Please be sure to answer the questionProvide details and share your research!Limit from the left Let f (x) f (x) be a function defined at all values in an open interval of the form (c, a), and let L be a real number If the values of the function f (x) f (x) approach the real number L as the values of x (where x < a) x < a) approach the number a, then we say that L is the limit of f (x) f (x) as x approaches a from theOn the graph of a function f (x), a vertical asymptote occurs at a point P = (x0,y0) if the limit of the function approaches ∞ or −∞ as x → x0 For a more rigorous definition, James Stewart's Calculus, 6th edition, gives us the following
When Does A Limit Exist Brilliant Math Science Wiki
How to find limit x approaches 0
How to find limit x approaches 0-Continuous at this point, then either the limit of f(x;y) as (x;y) approaches (x 0;y 0) does not exist, or this limit does exist but its value is not equal to 3 The reason is that the de nition of f being continous at this point is that the limit at this point exists and is equal to the value of the function at this point 4 Determine fFeb 13, 18 · In order for the limit to exist, you need the side limits to commute In this case which means that the side limits are equal and thus lim x → 0 x = 0 As far as the x x part, if you divide something by a quantity, you will also need to multiply it by that This is why you're getting 1 as a wrong answer there



Math 125 Review For Midterm 1 Spring 16 1
Jul 23, 15 · lim x→0− 1 x = − ∞ this means that the value of your function as you approach zero becomes enormous but negative (try using x = −001 or x = − ) 2 f (x) = 3x 1 as you approach zero from the right or left your function tends to 1!If x approaches 0 from the left, then the values of become large negative numbers In that case, we write When a function becomes infinite as x approaches a value c, then the function is discontinuous at x = c, and the straight line x = c is a vertical asymptote of the graphSep 17, · To do so, look at the graph and see the value f(x) is approaching as x approaches 0 We can see that as x gets closer and closer to 0, f(x), or the yvalue, gets closer and closer to 1 In other words, our answer is
9 rows · Here we say that lim x→0 g(x) = 1 Note that g(0) is undefined Graphical Approach toAnd say the lefthand limit of f(x) as x approaches a—or the limit of f(x) as x approaches a from the left—is equal to L if we can make the values of f(x) arbitrarily close to L by taking x to be sufficiently close to a and x less than a lim xa f x L o ONESIDED LIMITS Definition 2Limits, a foundational tool in calculus, are used to determine whether a function or sequence approaches a fixed value as its argument or index approaches a given point Limits can be defined for discrete sequences, functions of one or more realvalued arguments or complexvalued functions For a sequence {xn} { x n } indexed on the natural
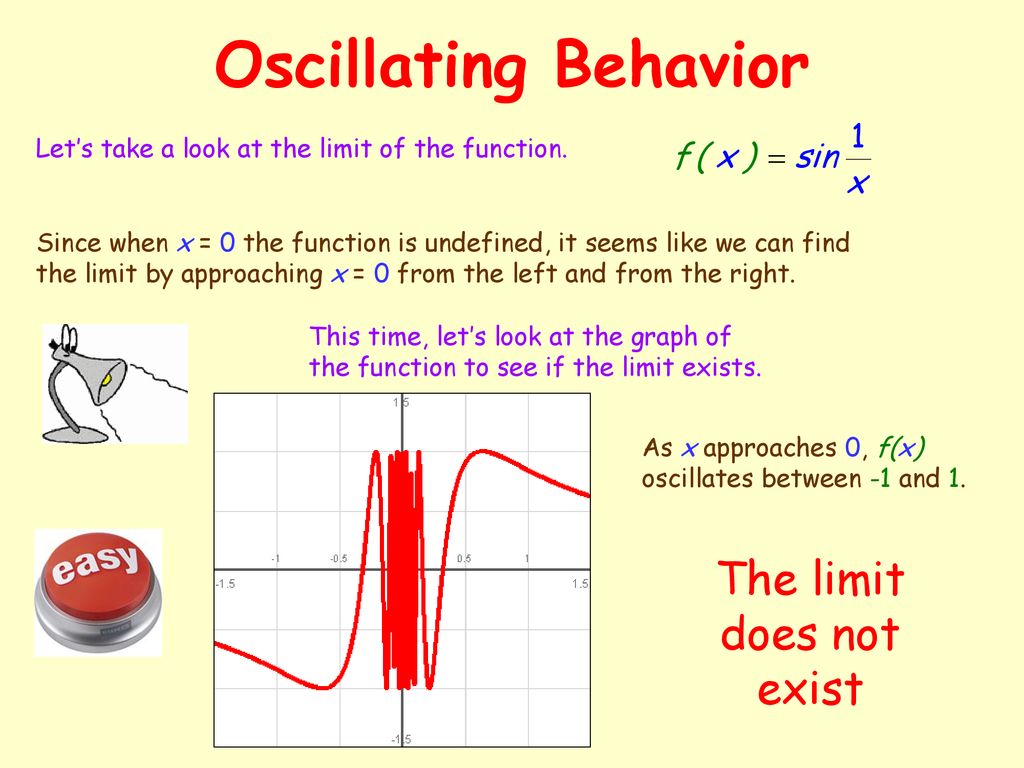
Something interesting happens when you examine $$f(x) = \sin\left(\frac 1 x\right)$$ as $$x$$ approaches 0 The function begins to oscillate faster and faster The function begins to oscillate faster and fasterAnswer lim x → ∞ f ( x) = ∞ Example 7 Use the graph below to understand lim x → ∞ x sin 2 ( 2 x) The oscillations of this function continue to increase in amplitude, but since the function always returns to the x axis, we can't say the limit is infinite Answer lim x → ∞ x sin 2Let's find the limit of f of X times H of X as X approaches zero all right and we have graphical depictions of the graphs y equals f of X and y equals H of X and we know from our limit properties that this is going to be the same thing as the limit as X approaches 0 of f of X x times the limit as X approaches 0 of H of X and let's think about what each of these are so let's first think about f of X right over here so on f of X is X approaches 0



Estimating Limit Values From Graphs Video Khan Academy




Introduction To Limits At Infinity Video Khan Academy
May 01, 17 · Graph of f 77 The figure above shows the graph of a function f with domain 0 x 4 Which of the following statements are true?But avoid Asking for help, clarification, or responding to other answersJun 13, 21 · Use the graph to investigate the limit of f(x) as x tends to 0 Let me see I gotta use the graph to investigate the limit of f(x) as x tends to 0 from the left and right Let y = f(x) The given function can also be expressed as f(x) = x The limit of (x) as x>0




Calculus For The Beginner Building Calculus Piece By Piece By Andre Ye The Startup Medium




Limits At Infinity Infinite Limits And Asymptotes
Evaluate lim xS0 S f 1x2, lim x 0S f 1 x2, and lim x 0 f 1 x2 T b Create a graph that gives a more complete representation of f 4 2 0 2 4 x 15 10 5 y 00 50 100 x 2 y Technology Exercises 49–56 Asymptotes Use analytical methods and/or a graphing utility to identify the vertical asymptotes (if any) of the following functions 49 fWe want to give the answer "0" but can't, so instead mathematicians say exactly what is going on by using the special word "limit" The limit of 1 x as x approaches Infinity is 0 And write it like this limx→∞ 1x = 0 In other words As x approaches infinity, then 1 x approaches 0Use a graphing utility, if possible, to determine the left and righthand limits of the functions f (x) f (x) and g (x) g (x) as x x approaches 0 If the functions have a limit as x x approaches 0, state it If not, discuss why there is no limit



The Indeterminate Form Ppt Download



What Is Calculus A Beginner S Guide To Limits And Differentiation Owlcation
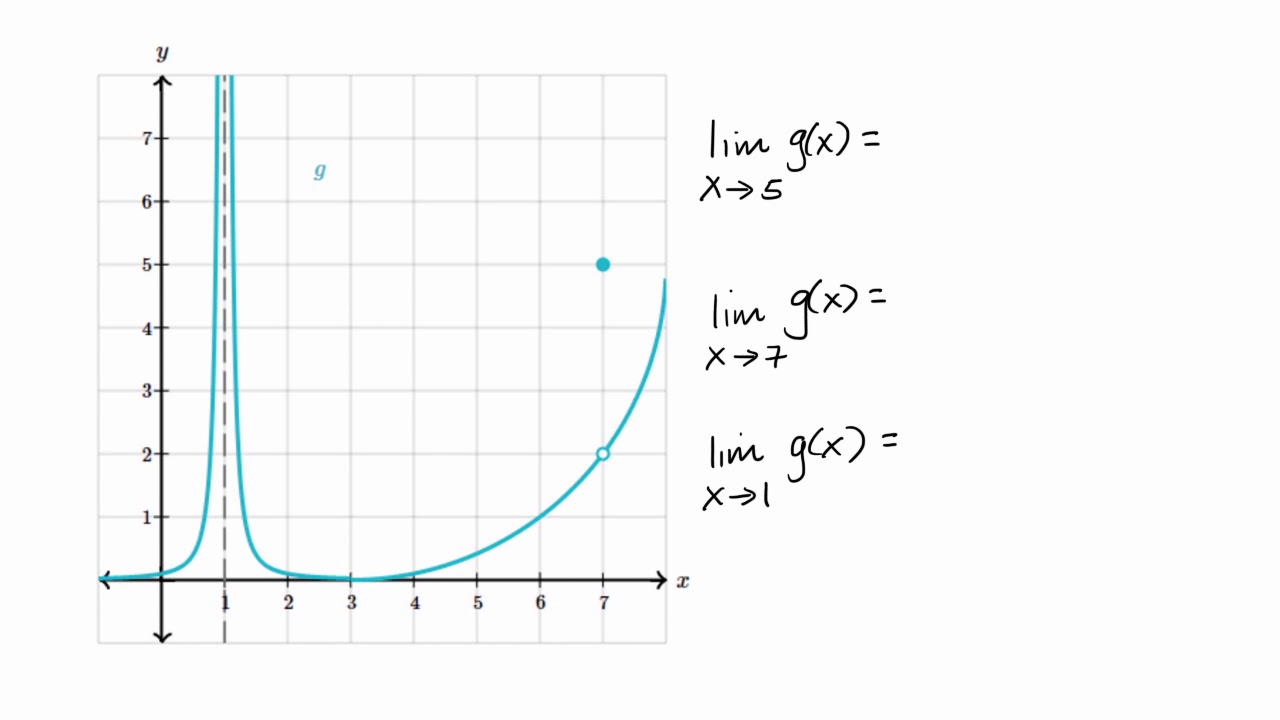
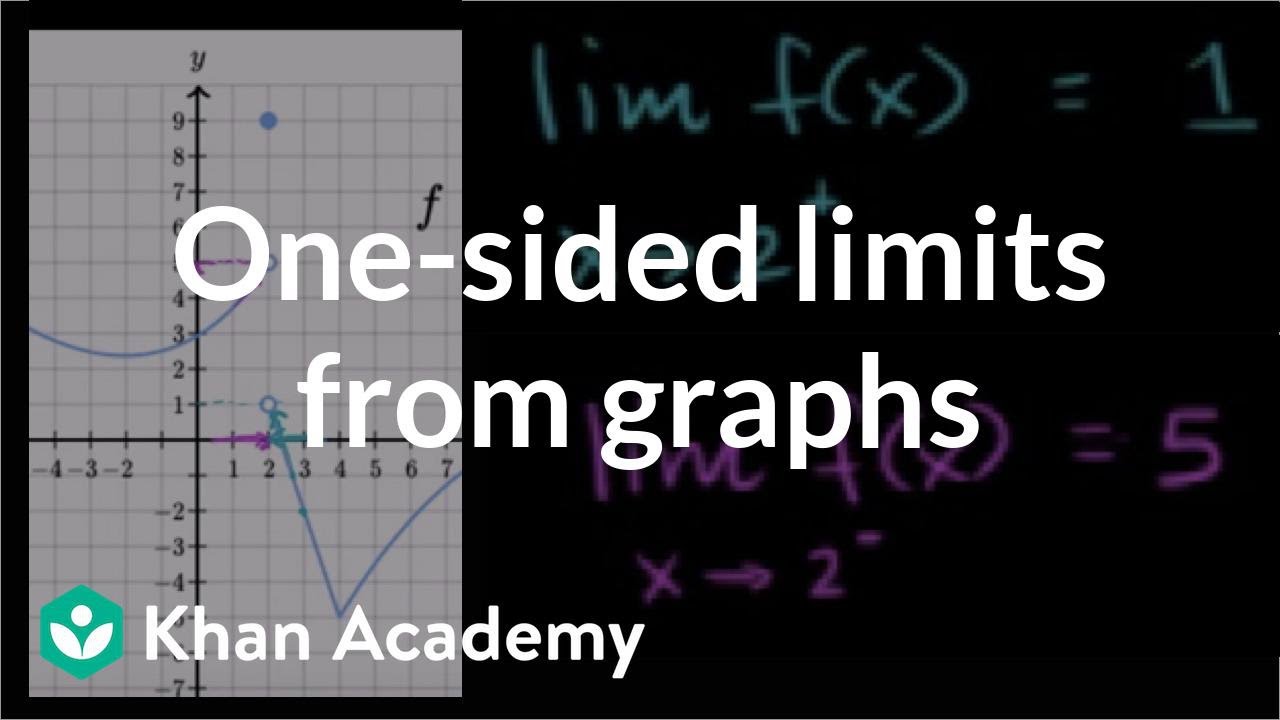
Get stepbystep solutions from expert tutors as fast as 1530 minutes Your first 5 questions are on us!For example, f (x)=x/x returns 1 for negative numbers, 1 for positive numbers, and isn't defined for 0 The onesided *right* limit of f at x=0 is 1, and the onesided *left* limit at x=0 is 1 Created by Sal Khan Google Classroom Facebook Twitter Email Estimating limit values from graphs Estimating limit values from graphsDec 21, · The function f(x) = ex is the only exponential function bx with tangent line at x = 0 that has a slope of 1 As we see later in the text, having this property makes the natural exponential function the most simple exponential function to use in many instances Figure 193 The graph of f(x) = ex has a tangent line with slope 1 at x = 0



What Is Calculus A Beginner S Guide To Limits And Differentiation Owlcation




Vertical Asymptote If F X Approaches Infinity Or Negative Infinity As X Approaches C From The Right Or The Left Then The Line X C Is A Vertical Asymptote Ppt Download
Evaluate limit as x approaches 4 of fx lim x→−4 f x lim x → 4 f x Move the term f f outside of the limit because it is constant with respect to x x f lim x→−4x f lim x → 4 x Evaluate the limit of x x by plugging in −4 4 for x xAs x gets really, really big, the graph gets closer and closer to the xaxis which has a height of 0 So, as x approaches infinity, f(x) is approaching 0 This is called a limit at infinityCalculus questions and answers;
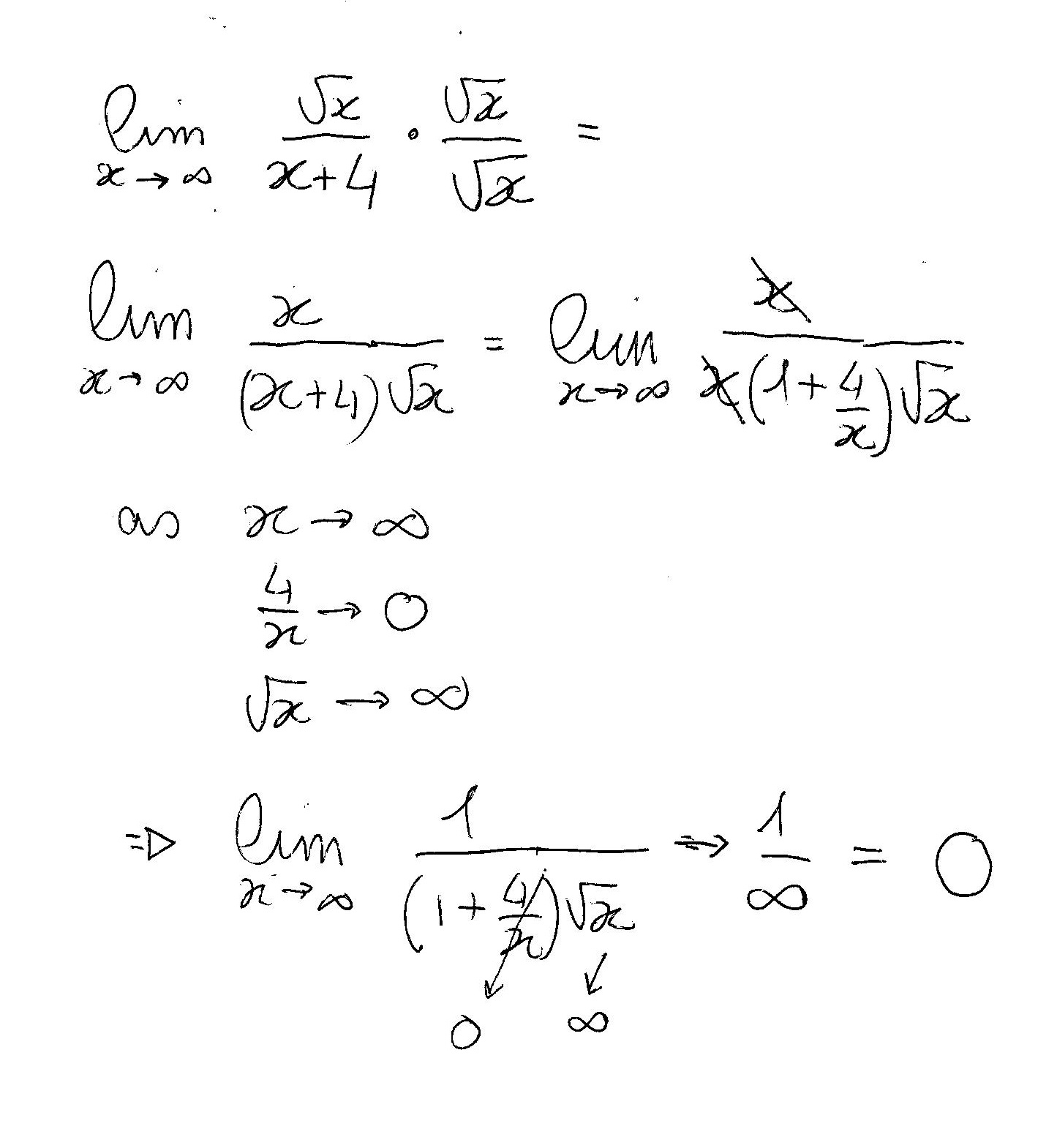



What Is The Limit Of Sqrt X X 4 As X Approaches Infinity Socratic




2 1 Introduction To Limits Ppt Download
Lim F X X Approaches 0 Graph Does The Limit As X Approaches 0 Of The Function 1 X 2 Exist It S My Understanding That It Is Not Continuous But Both The Left And Right Hand Limits Approach Infinity Quora For more information and source, see on this link httpsBasically, as a general rule, when you have to evaluate a limit for x → a try first toHere, we would say that the limit of f (x) as x approaches zero from the left is negative infinity and that the limit of f (x) as x approaches zero from the right is infinity The limit of f (x) as x approaches zero is undefined, since both sides approach different values




Solved 1 1st Picture The Steps Are In The 2nd And 3rd Chegg Com




Precalculus Concepts What Is A Limit Expii
I SHOULD HAVE BEEN WRITING LIMIT X TO 0 ALL THE WAY THROUGH, UNTIL I ACTUALLY EVALUATEDSome of the links below are affiliate links As an Amazon Associate IEvaluate limit as x approaches 6 of F (x) lim x→6 F (x) lim x → 6 F ( x) Move the term F F outside of the limit because it is constant with respect to x x F lim x→6x F lim x → 6 x Evaluate the limit of x x by plugging in 6 6 for x xNov 14, 15 · Graph of sin(π/x) with x axis changing from / 1 units to / 001 units This shows graphically the intuition the OP had that the frequency of the sine wave approaches infinity Share




1 3 1 3 The Limit Of A Function Math 181 The Limit Of Function First Motivation For Derivatives And Limits Tangent Line Problem Tangent Tangens Goal Define Studocu



What Is Calculus A Beginner S Guide To Limits And Differentiation Owlcation
But we can see that 1 x is going towards 0;Oct 06, · Thanks for contributing an answer to Mathematics Stack Exchange!Sketch the graph of a function f that satisfies the given values f(0) is undefined lim x > 0 f(x) = 4 f(2) = 6 lim x > 2 f(x) = 3 Solution From the given question, We understood that the functions is undefined when x = 0 When the value of x approaches 0 from left hand side and right hand side, limit value will approaches to 4



What Is The Limit Of E X E X X As X Tends To 0 Quora
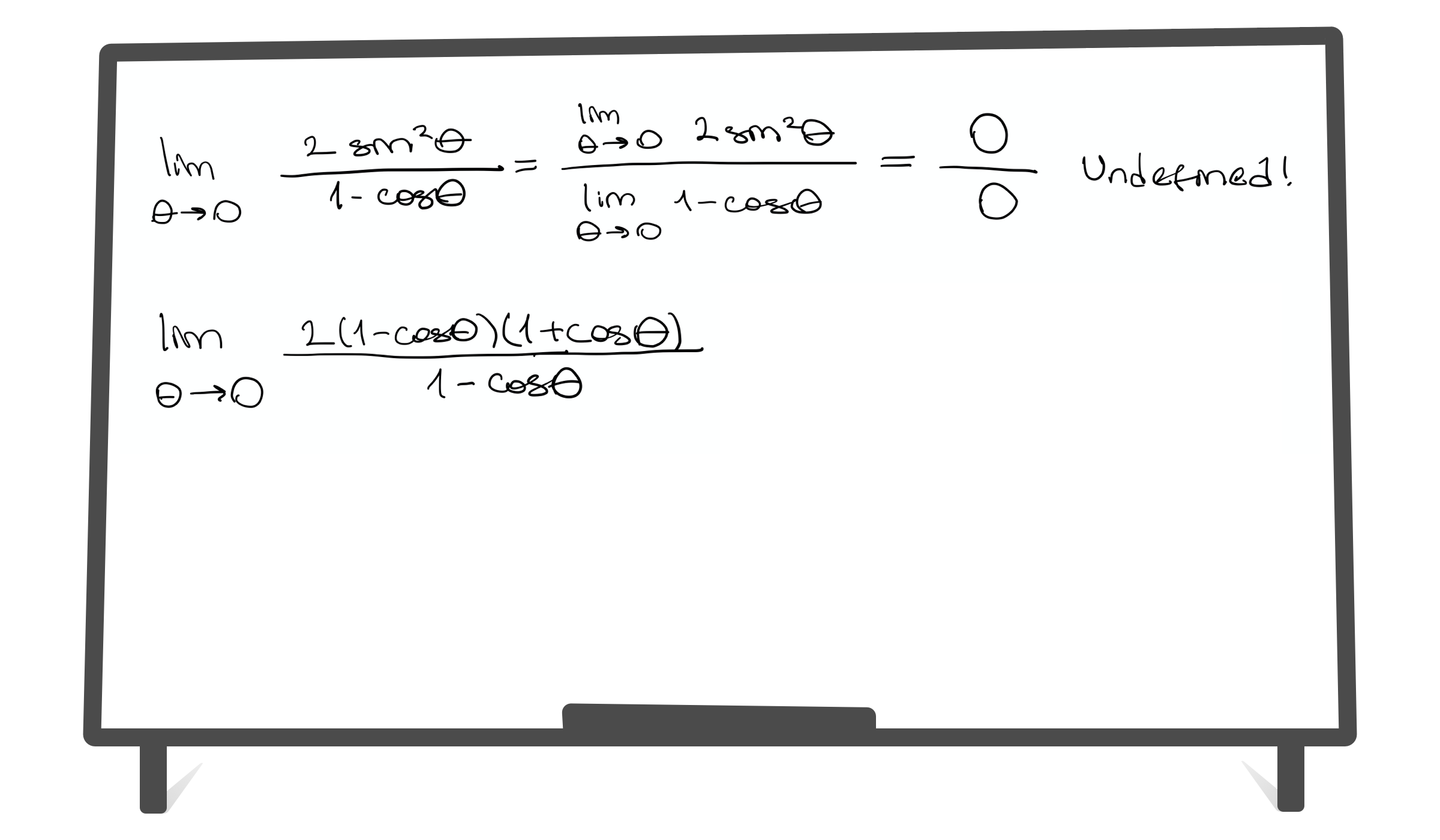



Limits Using Algebraic Manipulation By Can Balkaya Betamat En Medium
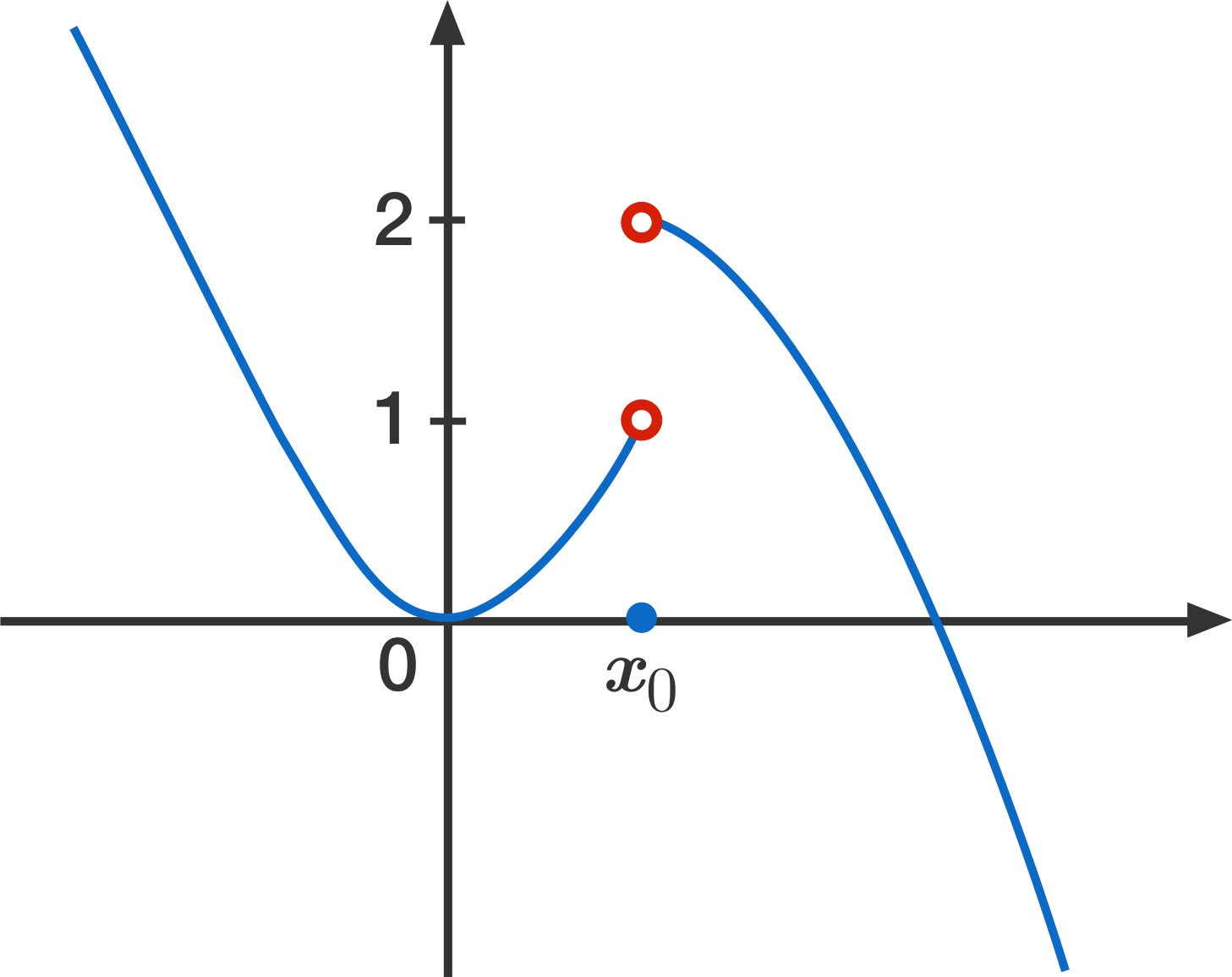
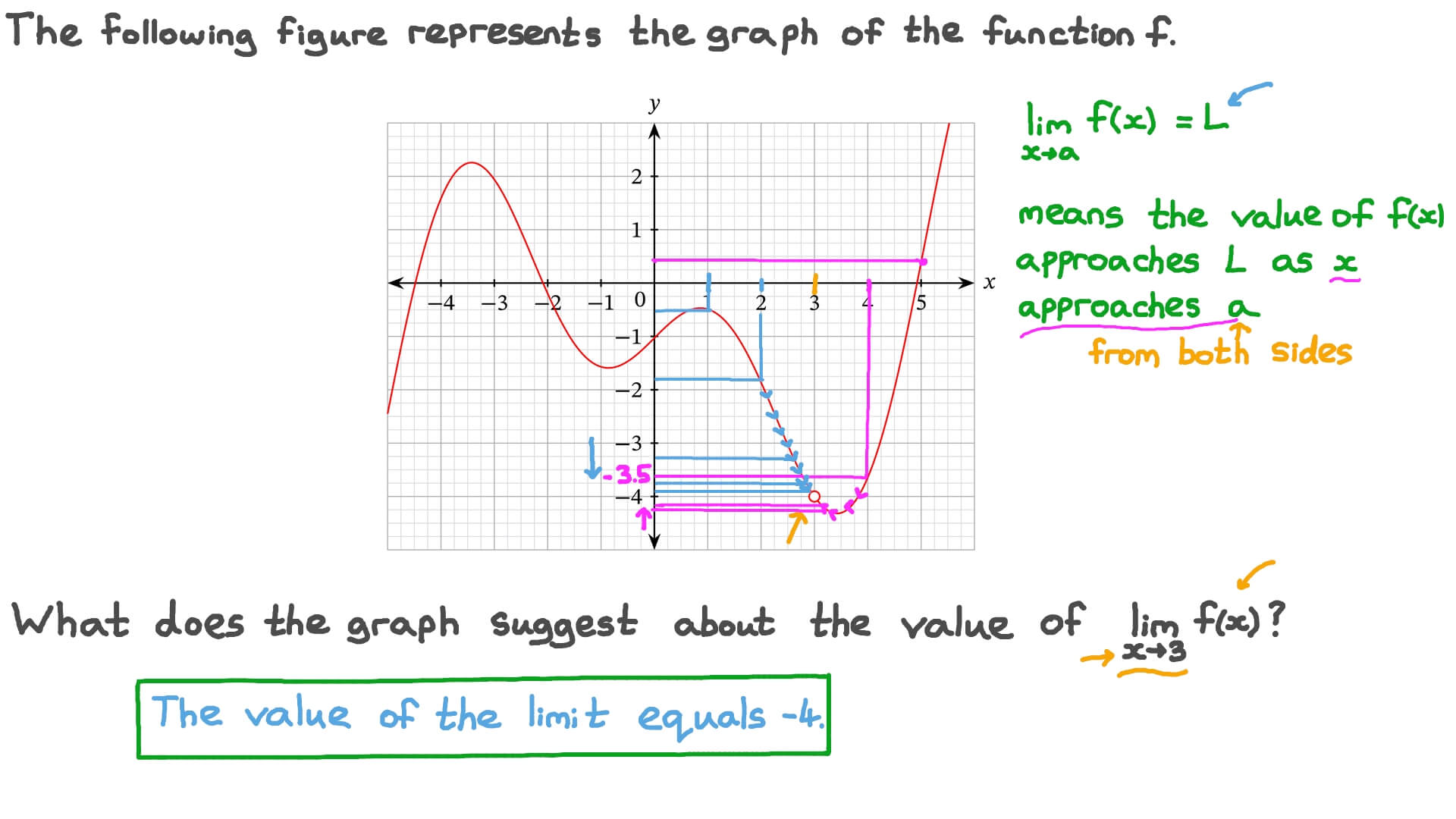
Solve limits stepbystep \square!If f f f does not jump or blow up at x 0 x_0 x 0 but lim x → x 0 f (x) \lim\limits_{x\to x_0} f(x) x → x 0 lim f (x) does not exist, the general picture is that f f f takes on multiple values which are far away from each other, even when its argument moves closer and closer to x 0 x_0 x 0{/eq} This could imply a vertical asymptote or a hole in the graph {eq}\displaystyle\lim\limits_{x\to 3} f(x) = 4 {/eq} This condition states that as {eq}x {/eq} approaches the value of {eq}3




Question 1 Multiple Choice Worth 2 Points Use The Given Graph To Determine The Limit If It Exists Brainly Com




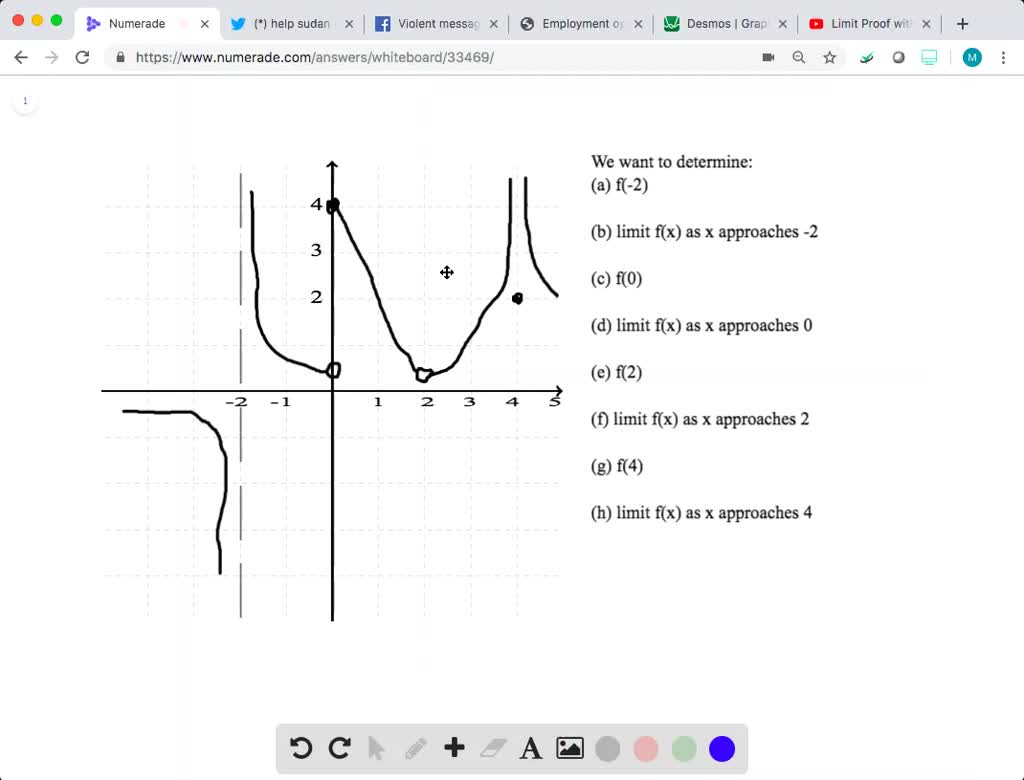
Solved 1 Let F X X2 X 6 X 3 Find Each Of The Fol Chegg Com
0 lim x x x → x x0 d 0 limsin x x π → ⎛⎞ ⎜⎟ ⎝⎠ i x y y 10 0 10 1 2 y1 1 x x0→ − lim f(x) = 1 and x0→ lim f(x) = 1 but since the two one –sided limits are not the same, → limf(x) DNE Neither side approaches a value, so we say the limit "does not exist" x0→ limf(x) DNE Neither side seems to approach a single value, so x0→ limf(x) DNEIf the existing limit is finite and having its x approaches for f(x) and for the same g(x), then it is the product of the limits A function f(x) usually contains the value of x but it is not compulsory Its best example is if f(x) = (x 4) (x 6)/2(x 6) is undefined at the value x = 6 because dividing by 2(6 6) = 0Lim x!0 x 2 sin(1=x) = 0, since the graph of the function is sandwiched between y = x2 and y= x2 O x K 1 K 05 0 05 1 K 1 K 05 05 1 Example Calculate the limit lim x!0 x 2 sin 1 x We have 1 sin(1=x) 1 for all x, multiplying across by x2 (which is positive), we get x2 x 2sin(1=x) x for all x, Using the Sandwich theorem, we get 0 = lim x!0 x
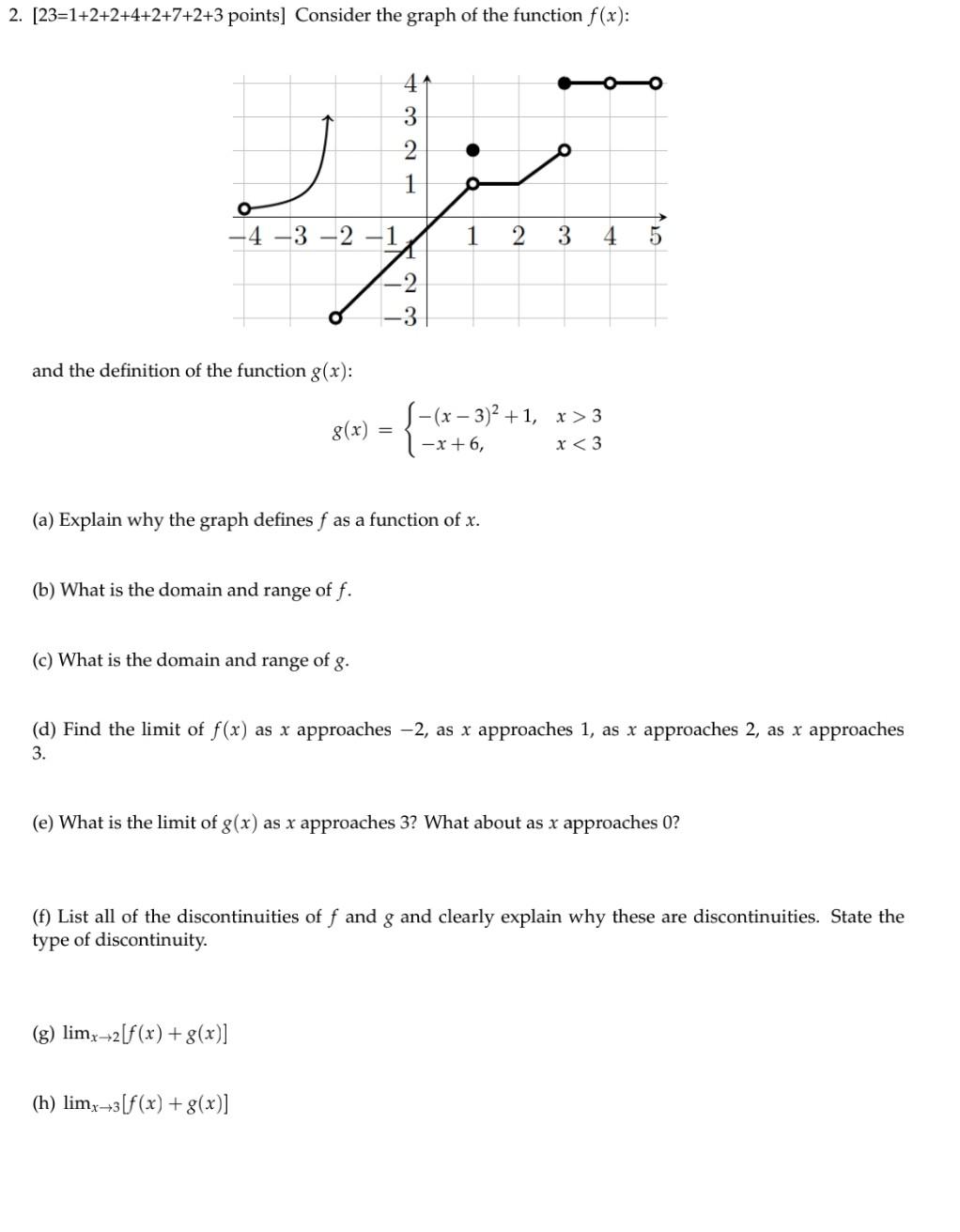



Solved 2 23 1 2 2 4 2 7 2 3 Points Consider The Graph Chegg Com




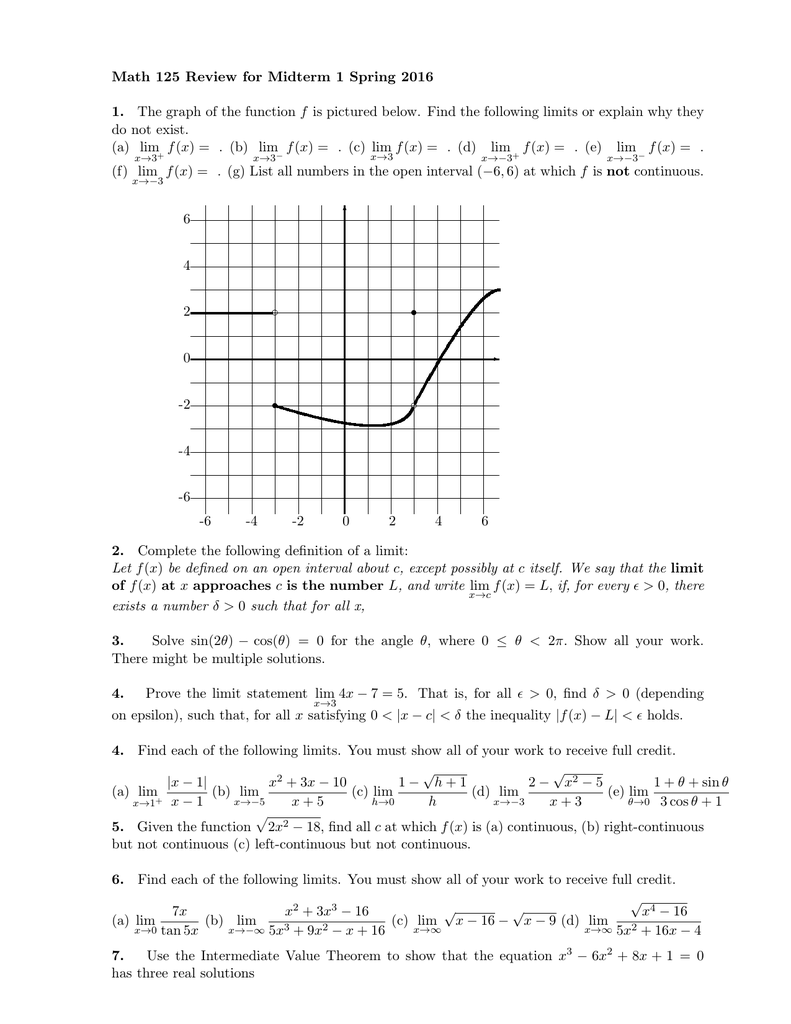
Math 125 Review For Midterm 1 Spring 16 1
16 Sketch the graph of a function f(x) that satisfies all the following conditions a) lim f(x)=0, lim f (x) = 3, lim f(x)=3 10 b) lim f(x) = lim f(x)= 0 lim f(x) = 5Nov 17, · As a motivating example, consider \(f(x) = 1/x^2\), as shown in Figure 130 Note how, as \(x\) approaches 0, \(f(x)\) grows very, very large It seems appropriate, and descriptive, to state that \\lim\limits_{x\rightarrow 0} \frac1{x^2}=\infty\Also note that as \(x\) gets very large, \(f(x)\) gets very, very smallLim x → ∞ f(x) = 0 lim x → ∞ f(x) = 0 An example with a function that has a limit of two at infinity For the function in the graph below, we first consider the behavior of f(x) as as x increases without bound, or in other words, we consider what happens to f(x) as we move farther and farther to the right on the graph




One Sided Limit Wikipedia




Chapter 14 Notes
From this we can guesstimate that the limit of f (x) = x 2 x − 1 as x approaches 0 is 2 lim x → 0 (x 2) x − 1 = − 2 While the limit of the function f (x) = x 2 x − 1 seems to approach 2 as x approaches 0 from either the left or the right, some function have only onesided limits The following notation is used to denoted lefthand and righthand limitsExample The graph of f(x) = sin(1=x) is shown below If we look at the behavior of the curve as xapproaches 0, we see that the graph oscillates between 1 and 1 with increasing frequency Since the y values on the graph do not approach a unique yvalue Las xapproaches 0, we have that lim x!0 sin(1=x) does not exist O O O (3) O O O O O (4) O OAs a result, limx→±∞r(x)/q(x)=0limx→±∞r(x)/q(x)=0 Therefore, the values of f(x)−g(x)f(x)−g(x)approach zero as x→±∞x→±∞ If the degree of p(x)p(x)is exactly one more than the degree of q(x)q(x)(n=m1),(n=m1),the function g(x)g(x)is a linear function In this case, we call g(x)g(x)an oblique asymptote



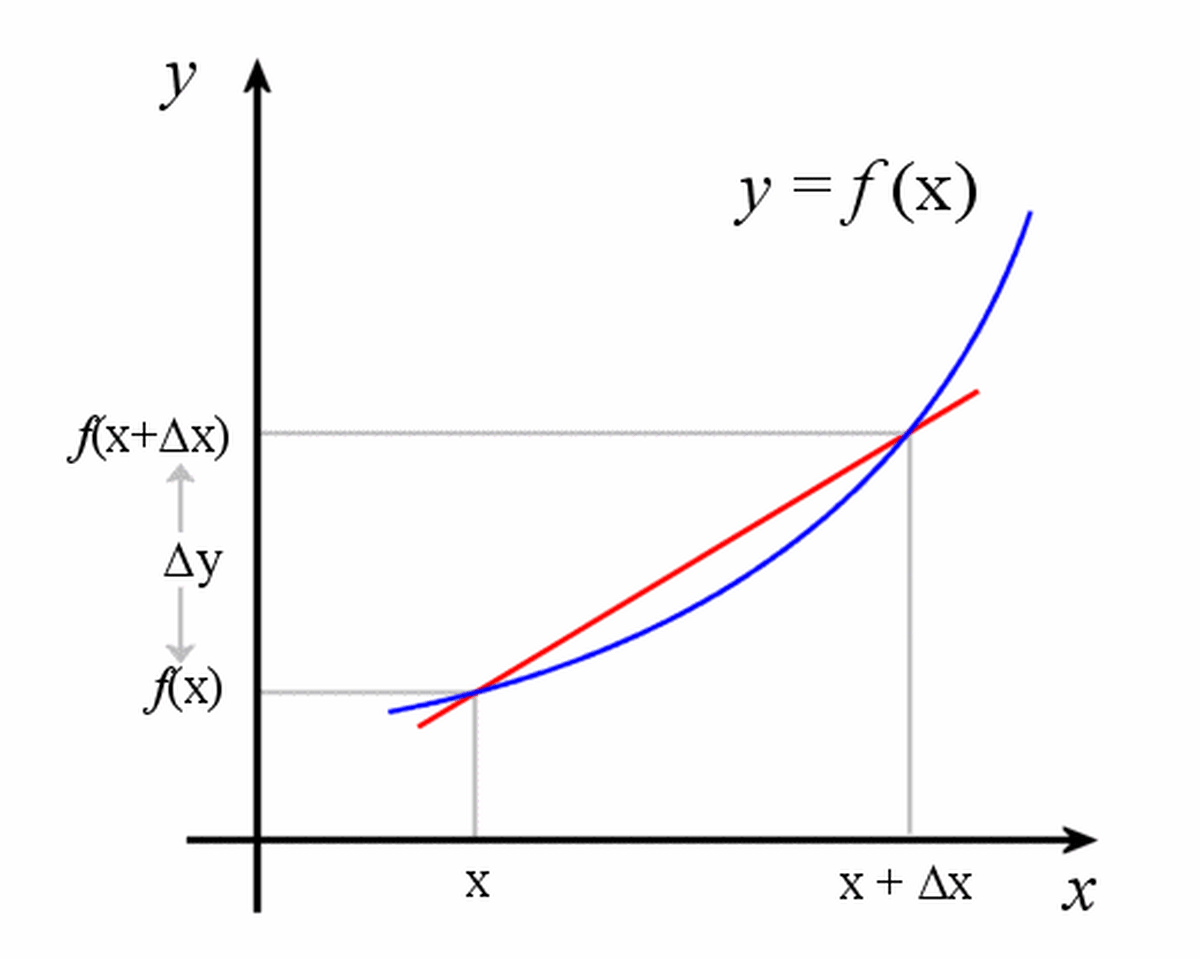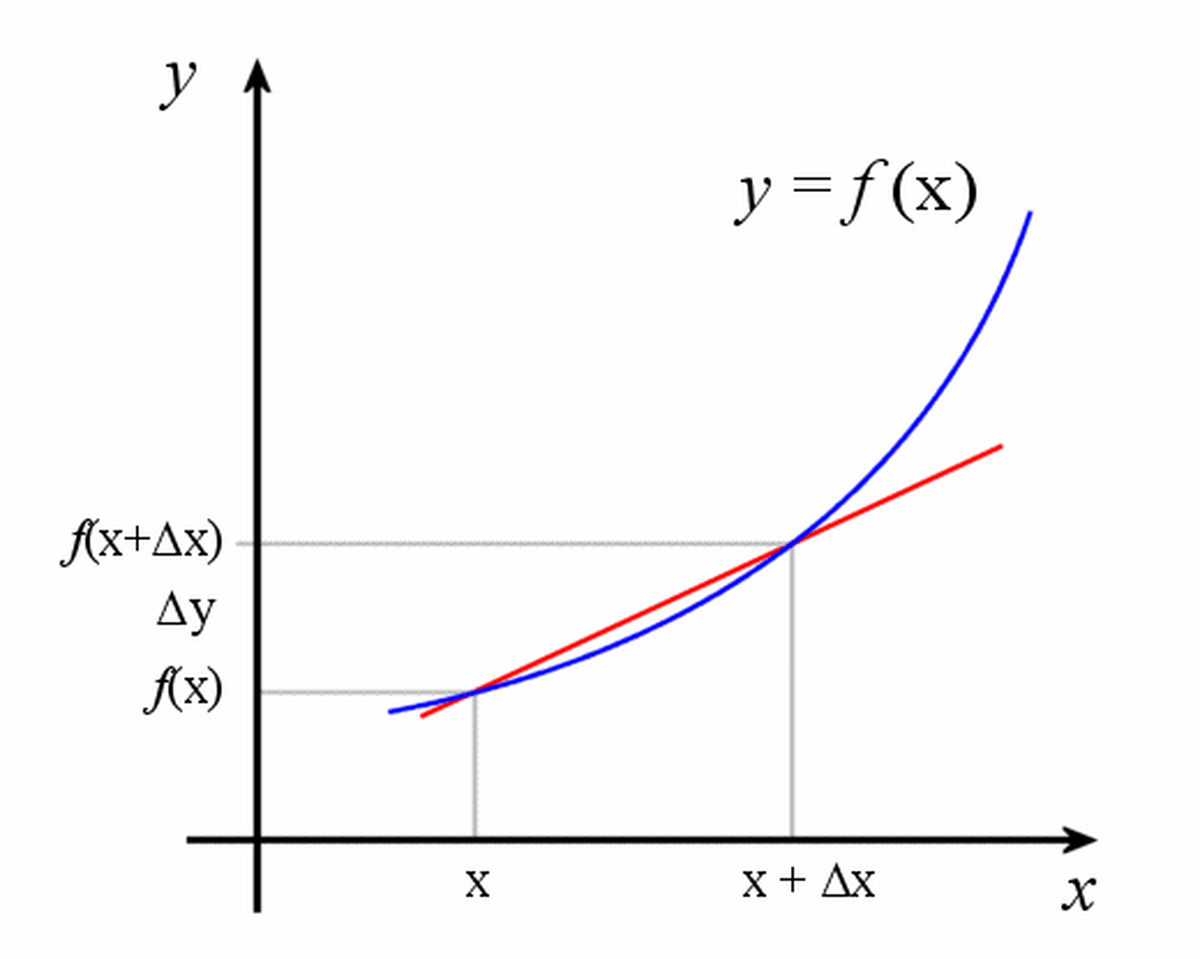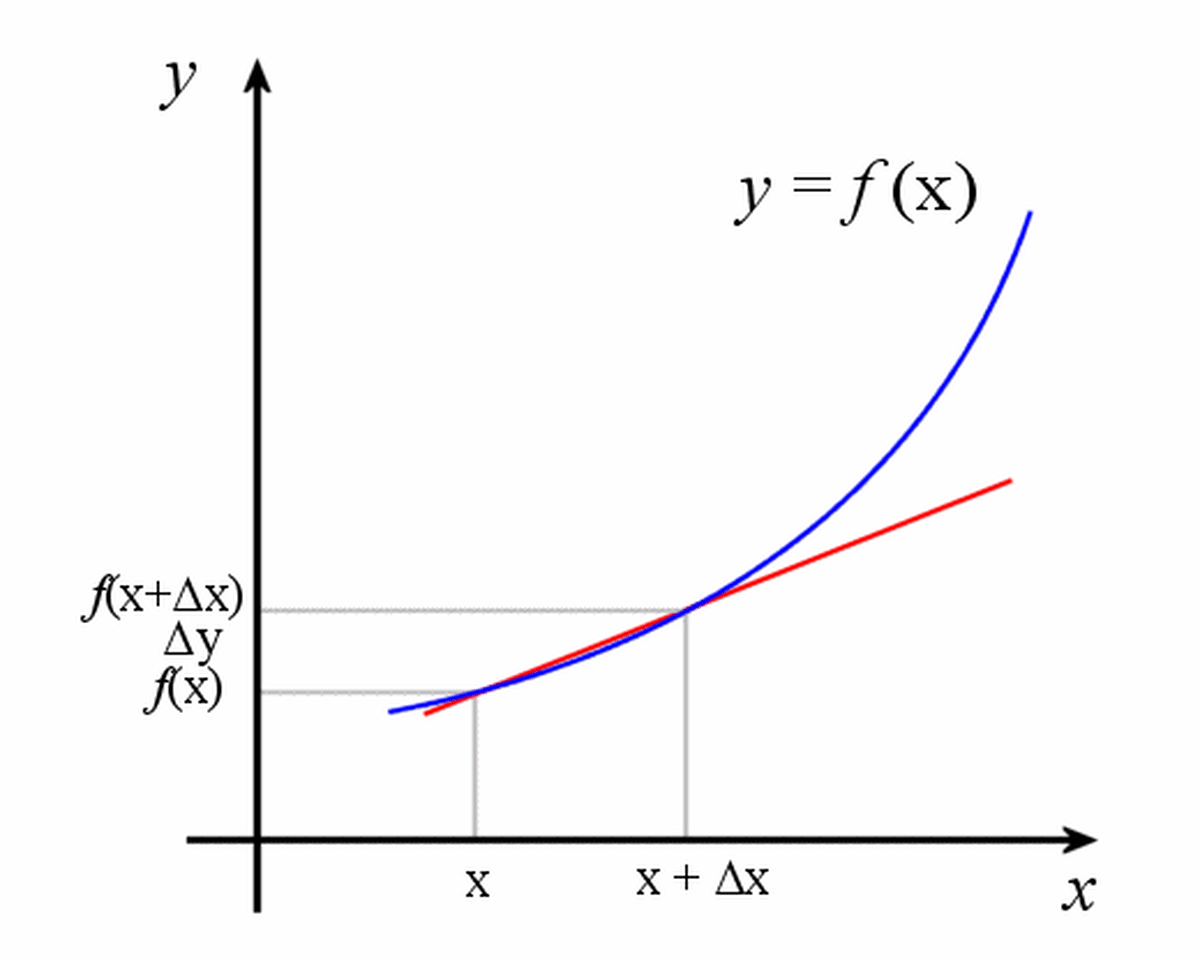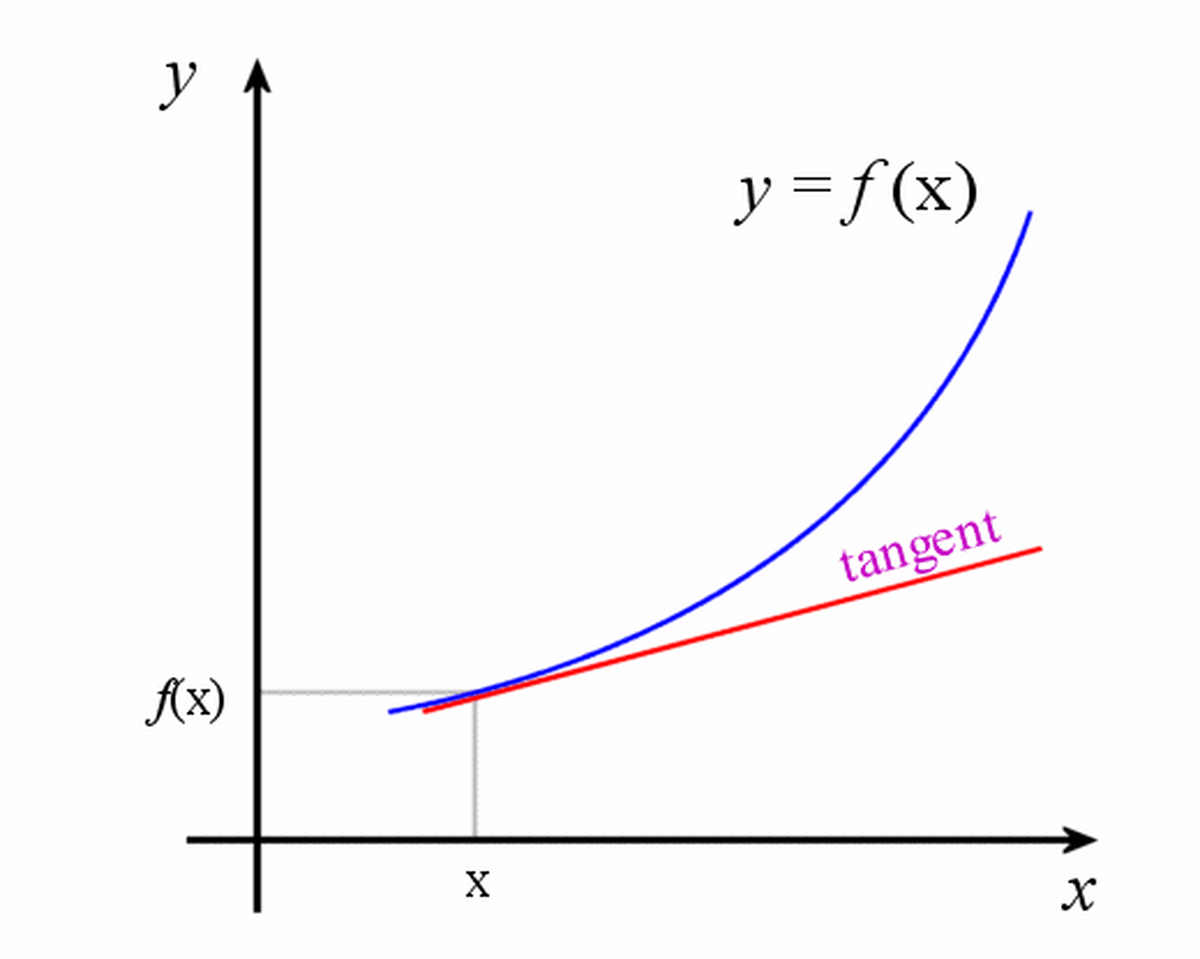
Maret School Calculus Derivative Defined As The Limit Of The Difference Quotient



Solved F Sketch The Graph Of F Sin F X Chegg Com
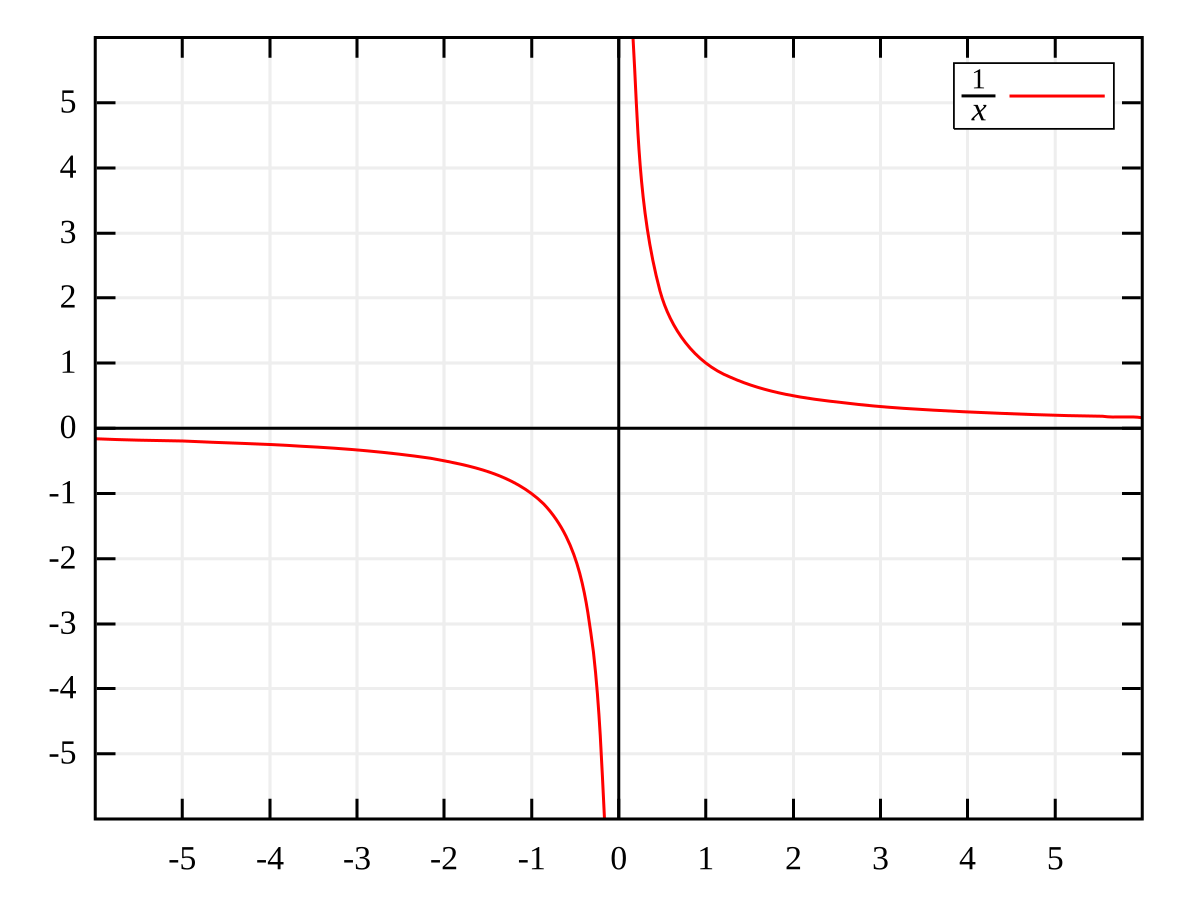
Dec , · Again we graph \(f(x)\) and create a table of its values near \(x=0\) to approximate the limit Note that this is a piecewise defined function, so it behaves differently on either side of 0 Figure 17 shows a graph of \(f(x)\), and on either side of 0 it seems the \(y\) values approach 1Condition Required for Existence of Limit of a Function lim x>x 0 f(x) = L exists if the following hold (i) lim x>x 0 f(x) exists, (ii) lim x>x 0 f(x) exists, and (iii) lim x>x 0 f(x) = lim x>x 0 f(x) = L Solved Problems Problem 1 Use the graph to find the limits (if it exists)N=1 are also points on the graph of the function f(x) = 1/x for x > 0 As x gets larger, f(x) gets closer and closer to zero In fact, f(x) will get closer to zero than any distance we choose, and will stay closer We say that f(x) has limit zero as x tends to infinity, and we write f(x) → 0 as x → ∞, or lim x→∞ f(x) = 0 5 10 x 0




When Does A Limit Exist Brilliant Math Science Wiki




Rational Functions
Answer to Use the graph to find the following lim f(x) as x approaches 2 lim f(x) as x approaches 0 lim f(x) as x approaches 5 fI lim f (E) exists IIS lim f (x) f(x) exists (B) 11 only (A) I only only (D) f(2) (E) 1, 11, and 79 Let f be a function such that lim I, f is continuous at x = 2 Il f is differentiable at x = 2X approaches 0 as x approaches zero and since ex approaches 1 as x Therefore, lim x→0 √ xex = 0 1 4 Exercise 2356 If lim x→0 f(x) x2 = 5, find the following limits (a) lim x→0 f(x) Answer The only way I can see how to do this is to reexpress what we want in terms Sketch a graph of the function Answer If f were




Solving Limits At Infinity Intuition And Examples




The Derivative
If lim f(x) = L1 as x approaches a from the left and lim f(x) = L2 as x approaches a from the right lim f(x) as x approaches a exists only if L1 = L2 Answer True This is an important property of the limits Question 9 True or False lim sin x as x approaches very large values (infinity) is 1 or 1If we have a graph of the function f(x) near x = c, then it is usually easy to determine lim x!c f(x) Example 1 Use the graph of y = f(x) given in the margin to determine the following limits (a)lim x!1 f(x) (b)lim x!2 f(x) (c)lim x!3 f(x) (d)lim x!4 f(x) Solution Each of these limits involves a different issue, as you may be able to tell




Which Statement Identifies And Explains Limit Of F X As X Approaches 0 Brainly Com




Limit Of X 2 1 Cos X As X Approaches 0 Youtube




Connecting Limits At Infinity Notation And Graph Video Khan Academy



Calculus For The Beginner Building Calculus Piece By Piece By Andre Ye The Startup Medium




2 2 The Limit Of A Function In This Section We Will Learn Ppt Download




Limit As X Approaches 0 From The Right Of X X Youtube



1 1 A Preview Of Calculus And 1 Ppt Download




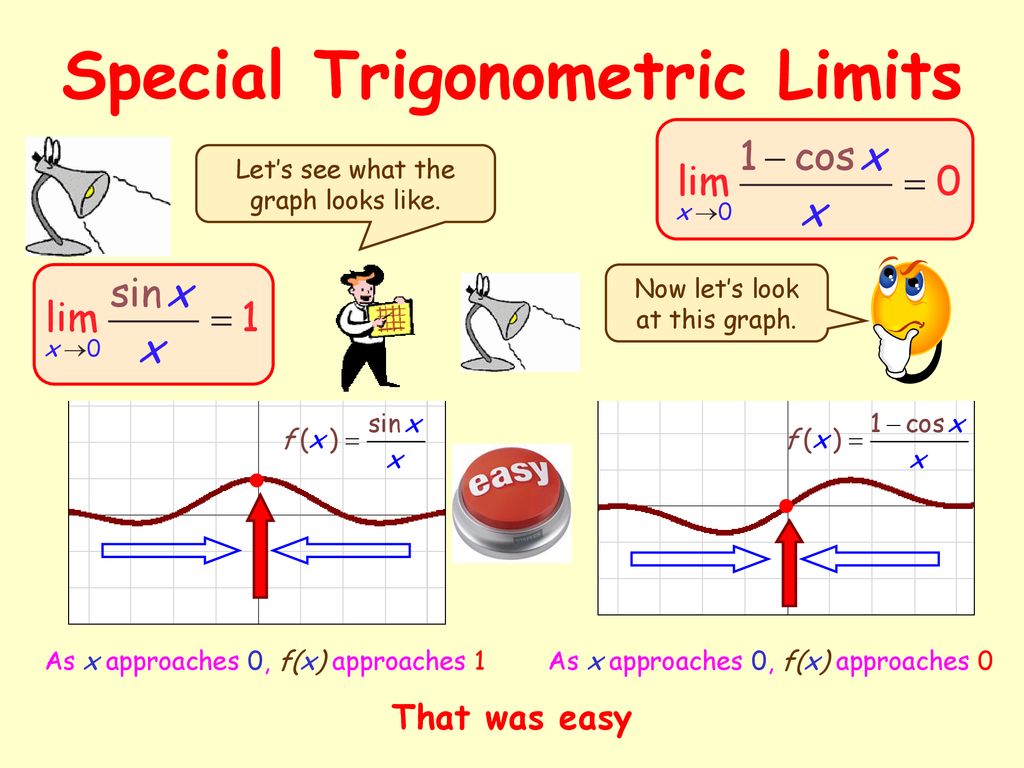
Limit Of 1 Cos X X As X Approaches 0 Youtube




Can Someone Please Explain Why The Answer To This Is 10 3 I Found The Derivative With Quotient Rule But I Am Still Getting X In The Denominator And I M Not Sure What



What Is Calculus A Beginner S Guide To Limits And Differentiation Owlcation




Answered A By Graphing The Function F X Bartleby




Limit Of 1 X 1 X As X Approaches 0 Youtube




Limits At Infinity Infinite Limits And Asymptotes




The Derivative




Limit Laws And Evaluating Limits Owlcation



Solved Graphical Reasoning In Exercises 29 And 30




Solved Example 5 Conditions Sketch A Possible Graph Of A Chegg Com




Math 019 Lecture 1 Section 2 1 Introduction To Limits Oneclass




Limit As X Approaches Infinity For Log Of Greatest Integer Over X Youtube



One Sided Limits From Graphs Video Khan Academy



Numerical Differentiation Wikipedia




Answered In X 1 Evaluate The Limit Of The Bartleby




Calculus For The Beginner Building Calculus Piece By Piece By Andre Ye The Startup Medium




14 2 Limits And Continuity



Division By Zero Wikipedia
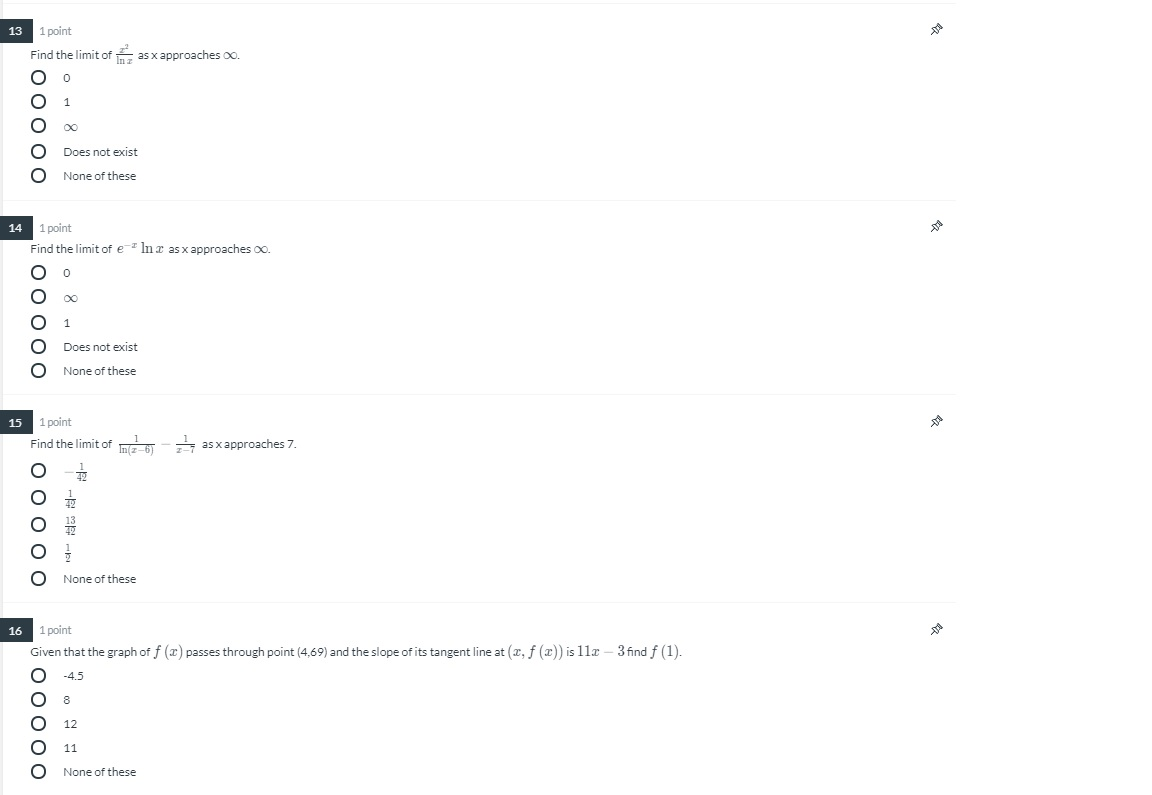



Solved As X Approaches 0 13 1 Point Find The Limit Off O Chegg Com
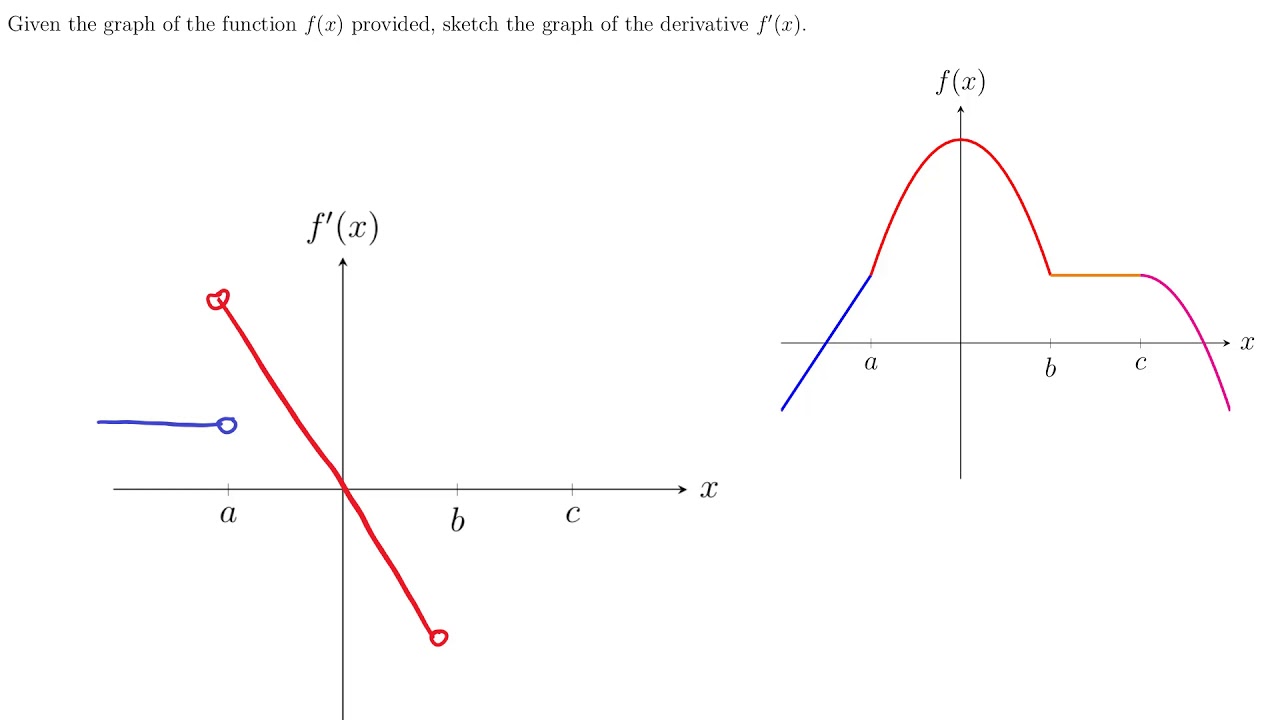



The Derivative Function



Calculus Limit Function Take The Limit As X Approaches
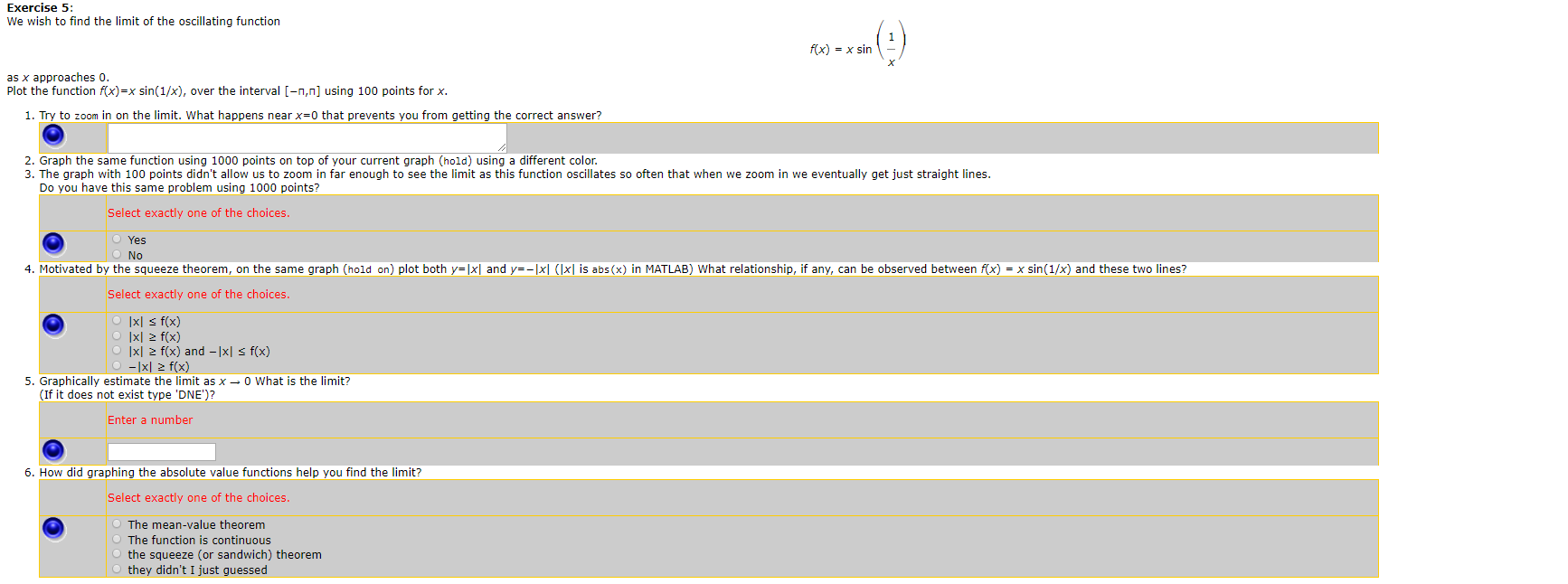



Solved Exercise 5 We Wish To Find The Limit Of The Oscil Chegg Com




L Hopital S Rule Wikipedia



What Is The Limit Of E X E X X As X Tends To 0 Quora
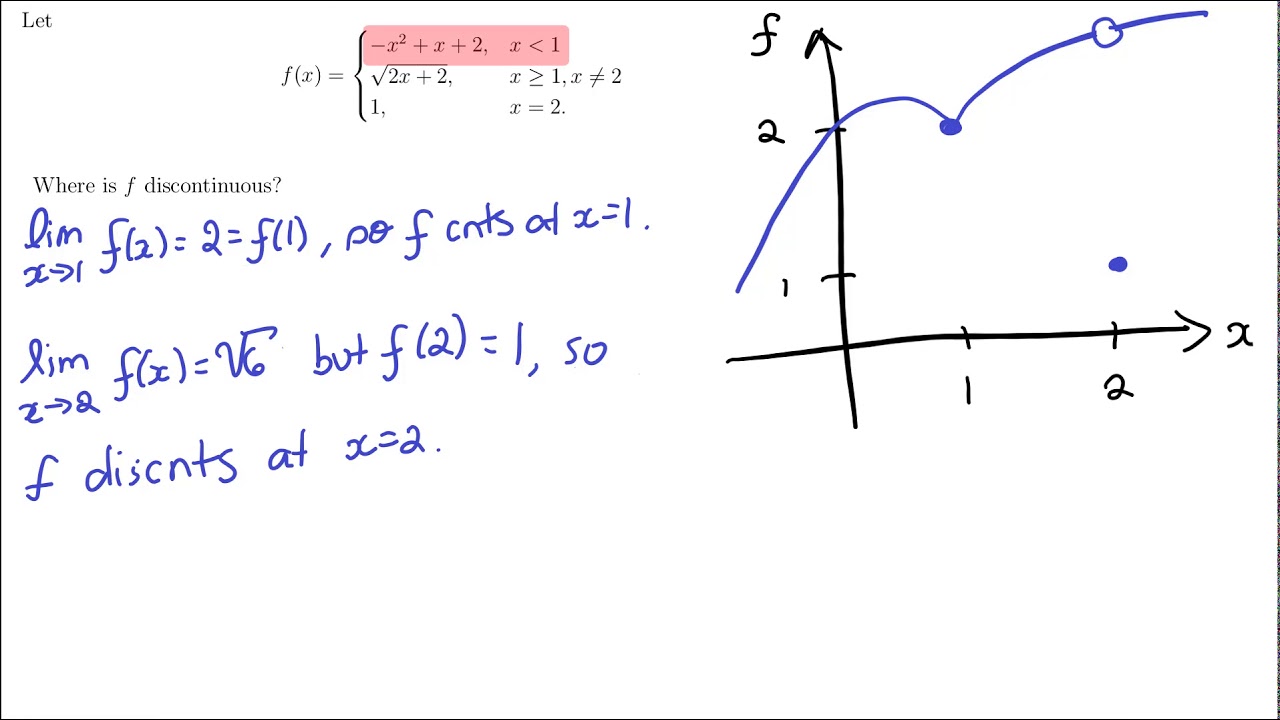



Continuity And Ivt




1 1 A Preview Of Calculus And 1 Ppt Download
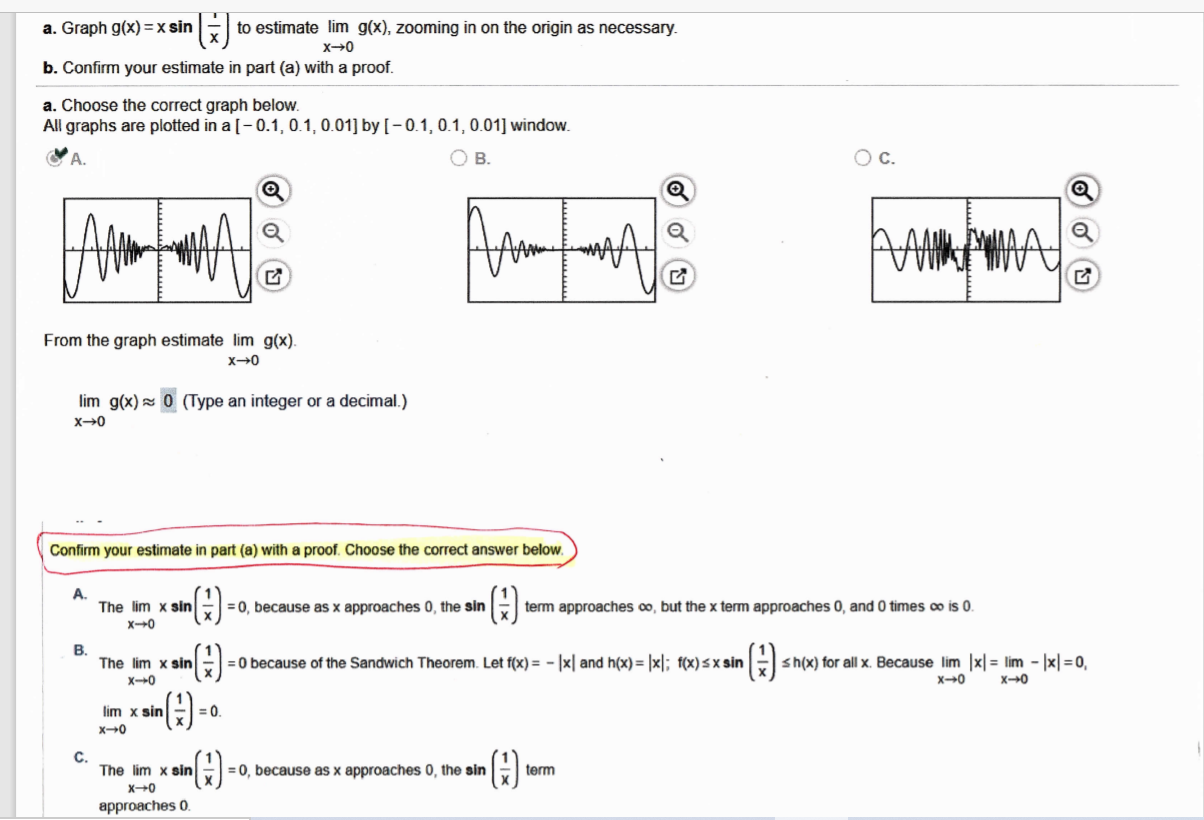



Answered A Graph G X X Sin To Estimate Lim Bartleby
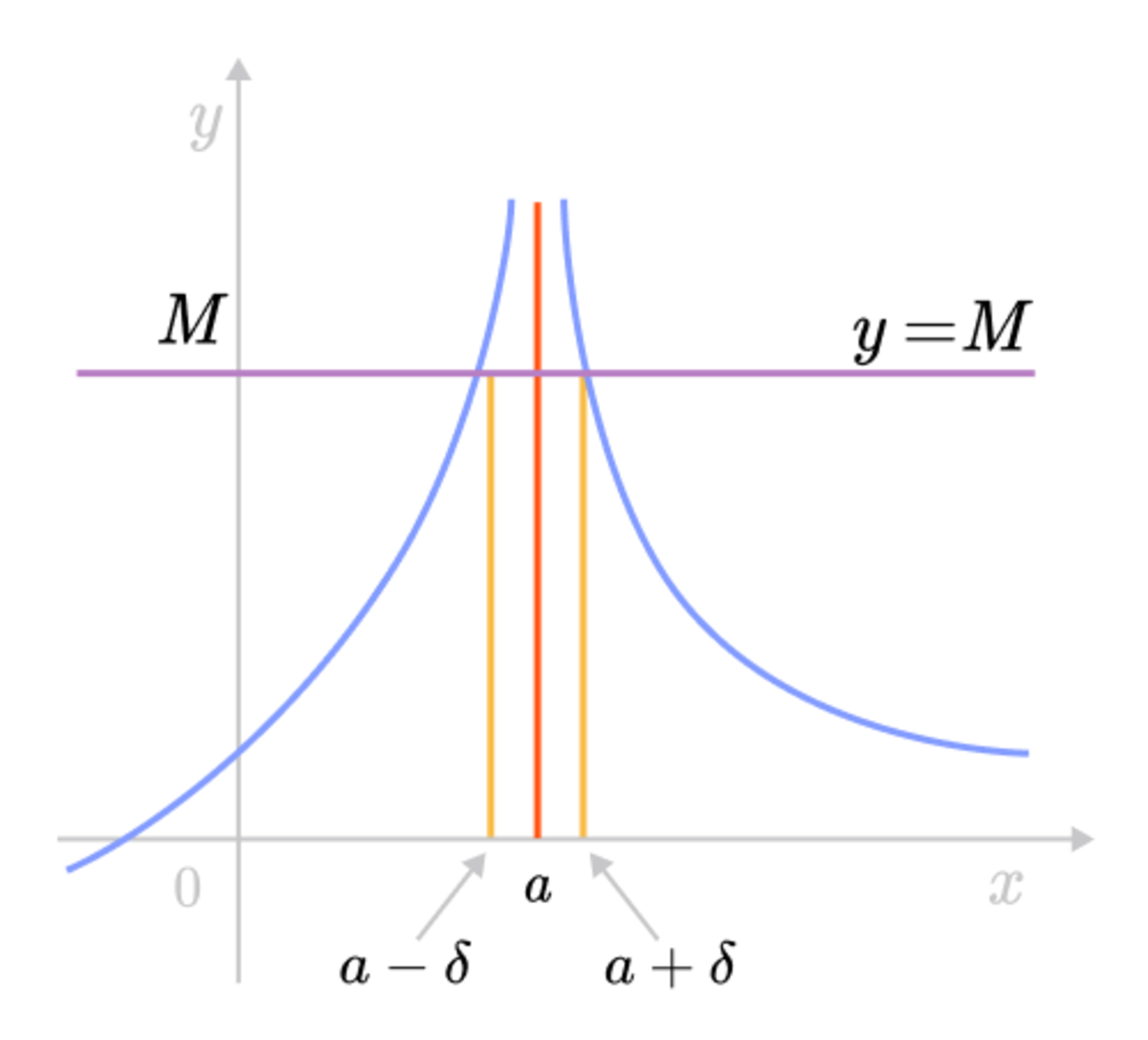



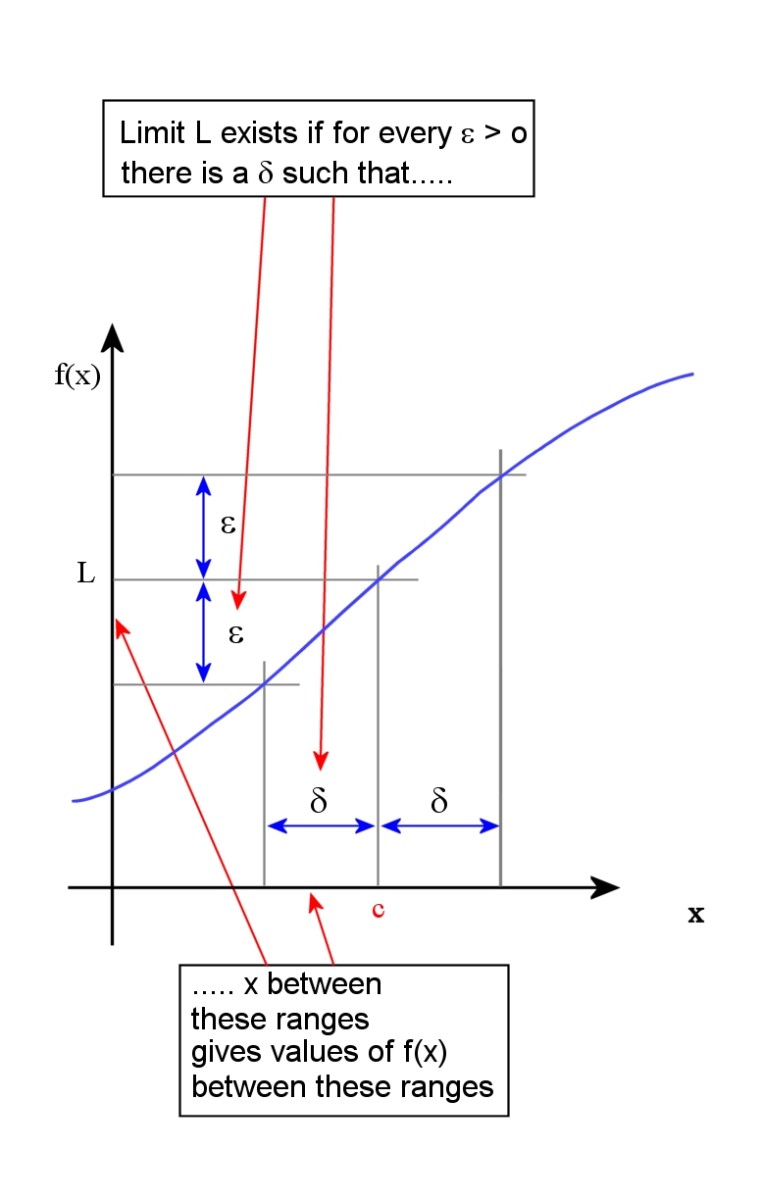
Epsilon Delta Definition Of A Limit Brilliant Math Science Wiki
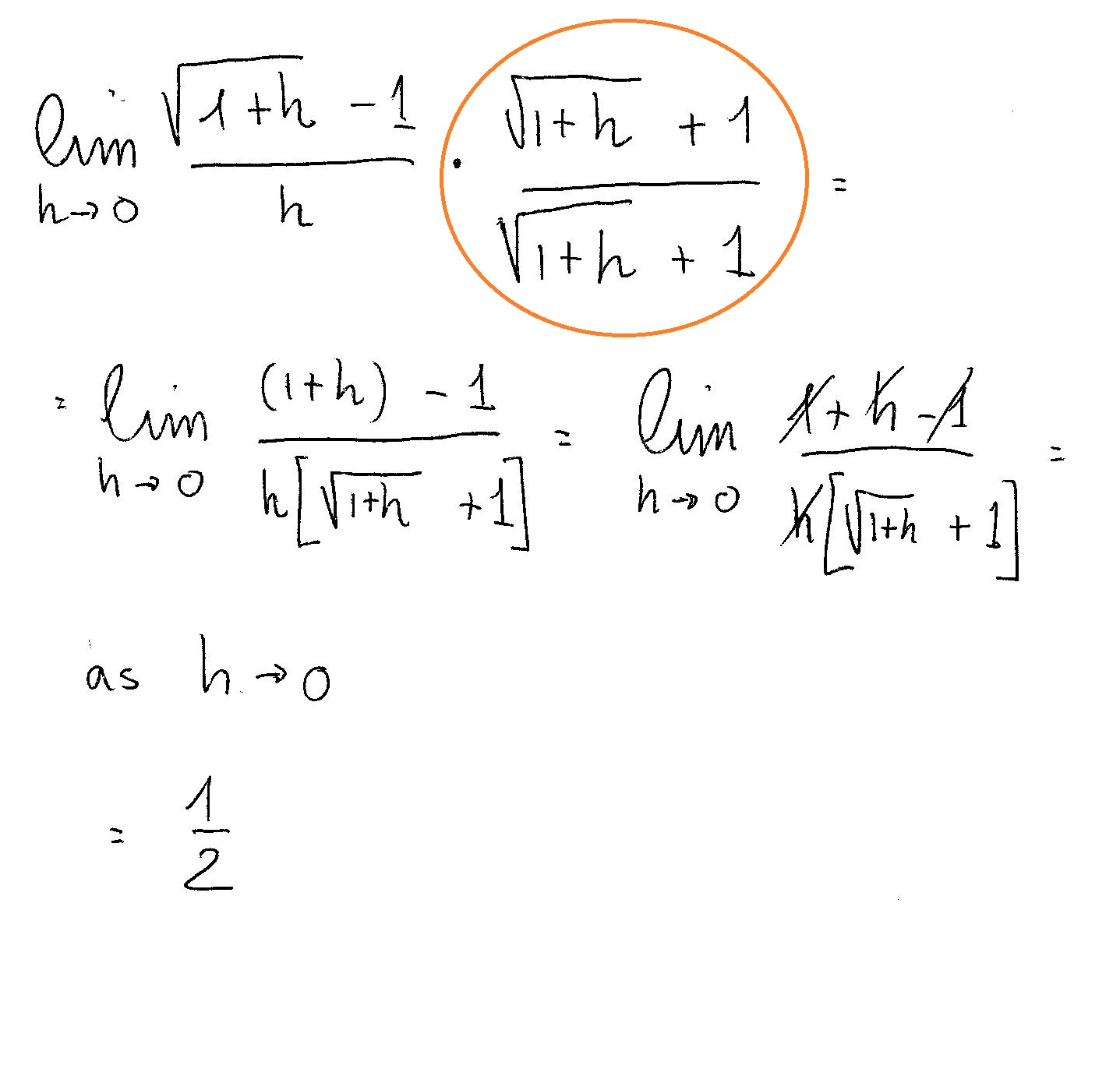



How Do You Find The Limit Of Sqrt 1 H 1 H As H Approaches 0 Socratic




Infinite Limit Laws
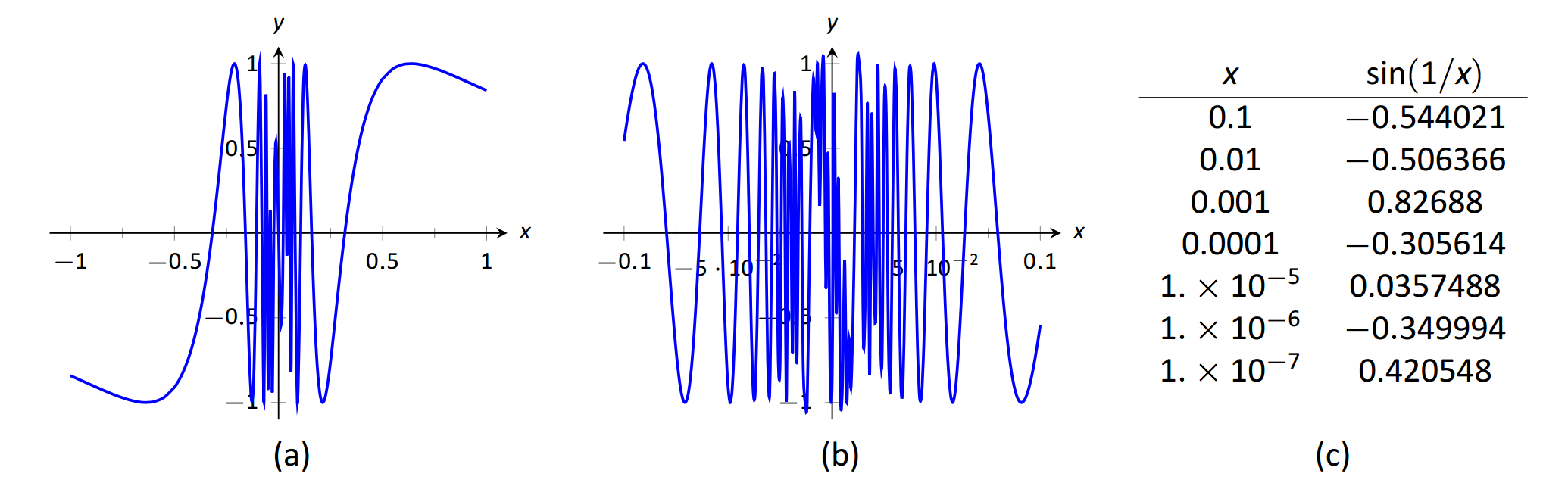



1 1 An Introduction To Limits Mathematics Libretexts
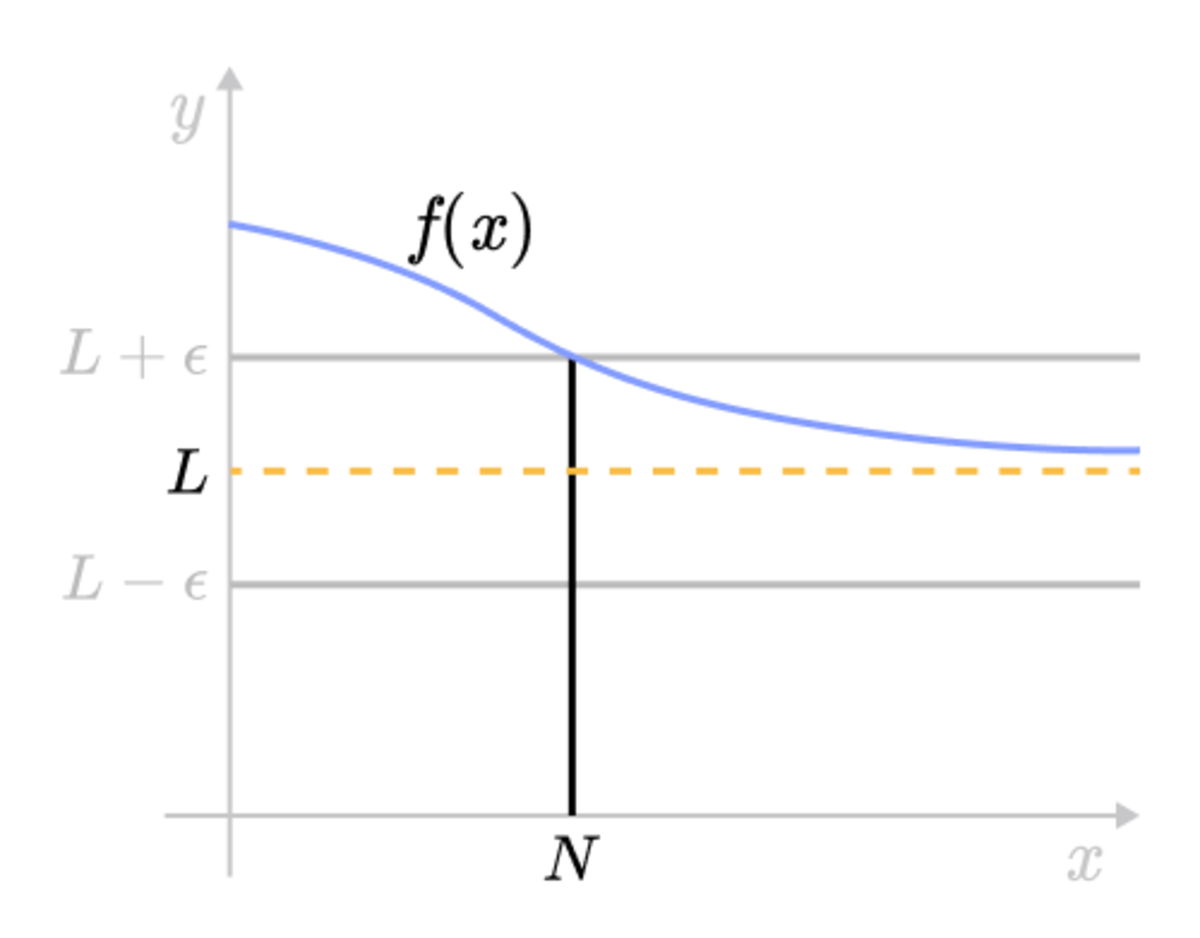



Epsilon Delta Definition Of A Limit Brilliant Math Science Wiki



1 6 Limits Involving Infinity Mathematics Libretexts
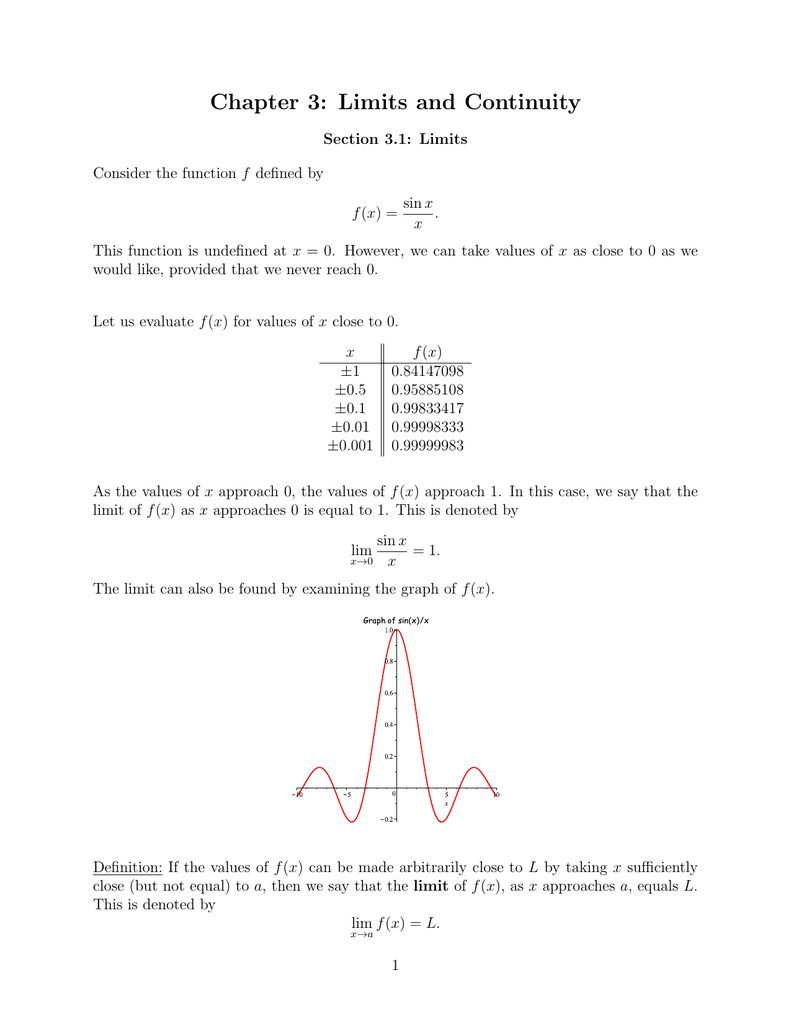



Chapter 3 Limits And Continuity



Calculus The Definition Of The Derivative



Calculus Limits
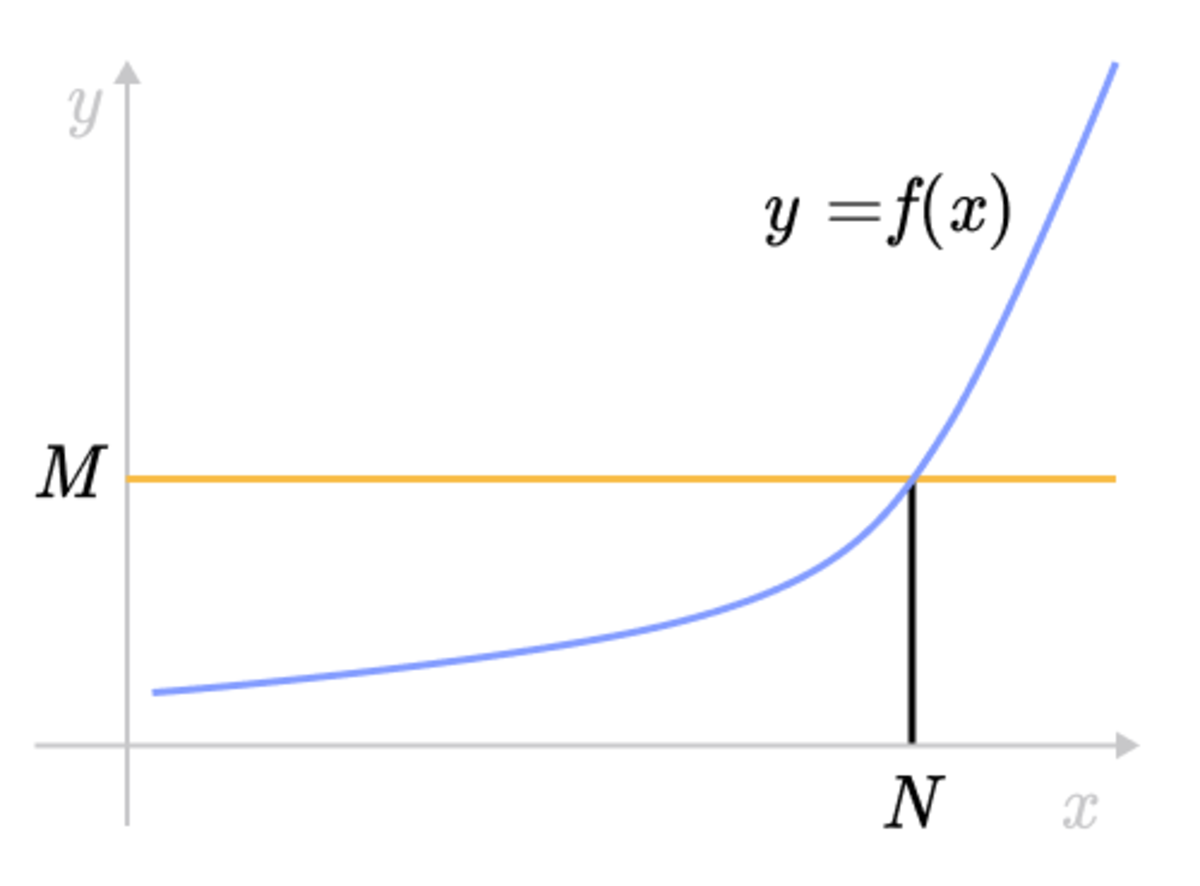



Epsilon Delta Definition Of A Limit Brilliant Math Science Wiki



The Burning Question What Is Calculus Ppt Download




Solving Limits At Infinity Intuition And Examples




Warm Up Exercse 2 1 Polynomials And Rational Functions Pdf Free Download



Maret School Calculus Derivative Defined As The Limit Of The Difference Quotient




E D Definition Of Limit Wikipedia




Trig Limits Trigonometric Functions Sine



Question Video Finding The Value Of A Limit From A Graph Nagwa




Solving Limits At Infinity Intuition And Examples




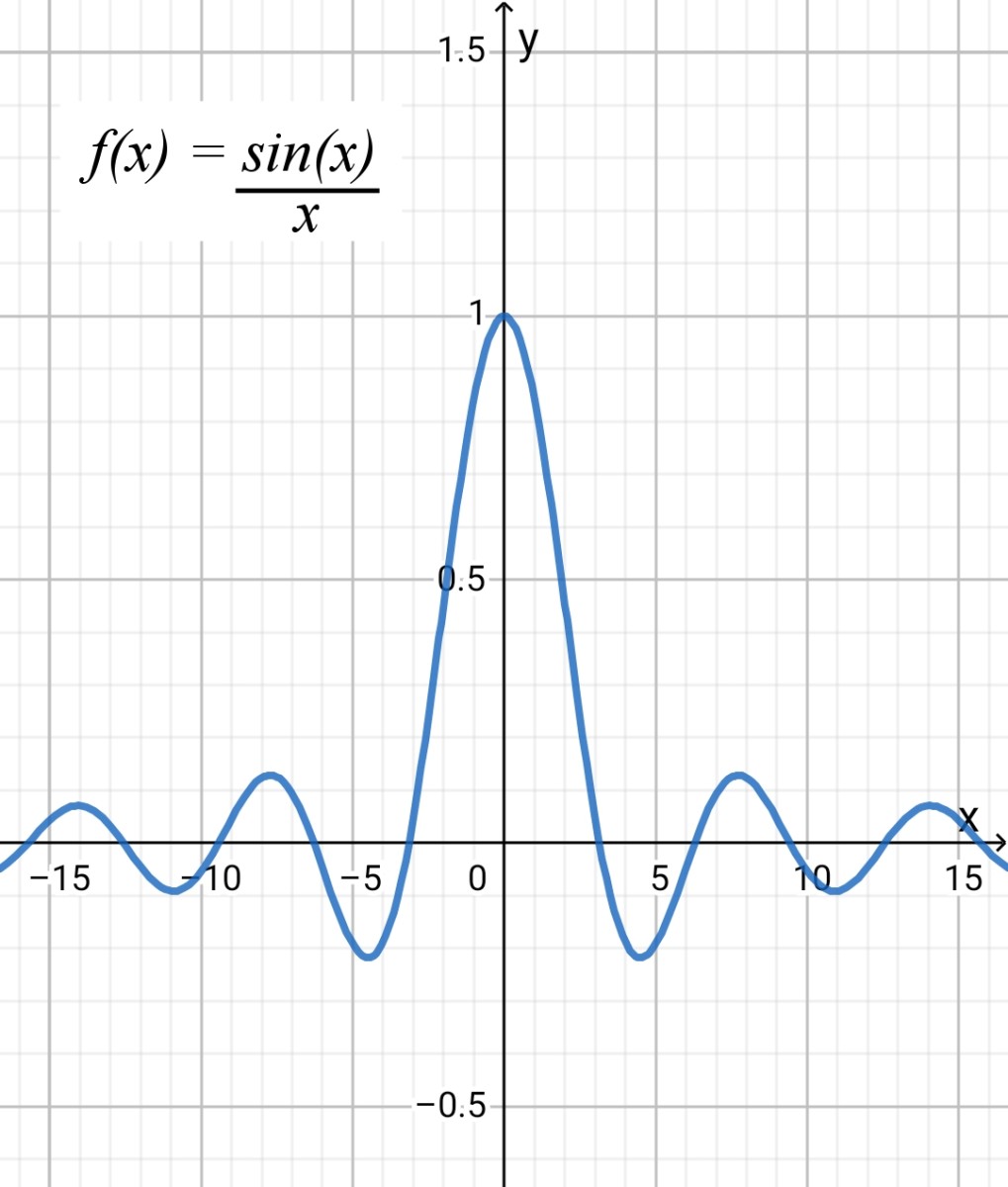
Limit Of Sin X X As X Approaches 0 Video Khan Academy




Limit Of 1 Cos X X As X Approaches 0 Video Khan Academy



2 8 17 Hw2 2 Http Www Webassign Net Web Student Assignmentresponses Last Dep 1 18 Webassign




Theorem For Limits Of Composite Functions Video Khan Academy



Question Video Discussing The Continuity And Differentiability Of A Piecewise Function At A Point Nagwa



Calculus Limits Using Tables Youtube



No comments:
Post a Comment