In three dimensions, as in two, vectors are commonly expressed in component form, v= x,y,z , or in terms of the standard unit vectors, xiyjzk Properties of vectors in space are a natural extension of the properties for vectors in a plane Let v= x_1,y_1,z_1 and w= x_2,y_2,z_2 be vectors, and let k be a scalarSimple and best practice solution for xyz=3 equation Check how easy it is, and learn it for the future Our solution is simple, and easy to understand,Using the above identity taking a = x − y, b = y − z and c = z − x, we have a b c = x − y y − z z − x = 0 then the equation (x − y) 3 (y − z) 3 (z − x) 3 can be factorised as follows
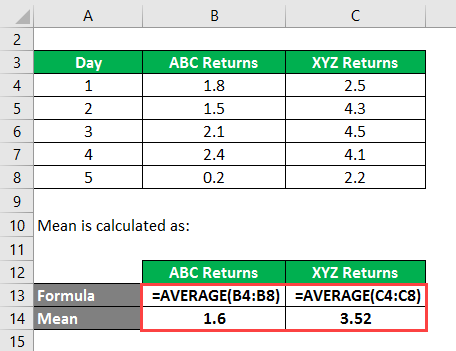
Covariance Formula Examples How To Calculate Correlation
(x y z)^3 formula
(x y z)^3 formula-There are two formula of it x^3 y^3 z^3 3xyz = (xyz) (x^2y^2z^2xyyzzx) 2 x^3 y^3 z^3 3xyz = (1/2) (xyz) {xy)^2(yz)^2(zx)^2}In case of a rectangular coordinate system, it is given by an ordered 3tuple (x, y, z) Also, if the coordinates (x, y, z) is already known, then we can easily locate the point P in space The concept of section formula can be extended to threedimension geometry as well as to determine the coordinates of a point dividing a line in a certain



Surface Area
X 2 y 2 z 2 = r 12 (x d) 2 y 2 z 2 = r 22 Subtracting the first equation from the second, expanding the powers, and solving for x gives x = d 2 r 22 r 12 / 2 d The intersection of the two spheres is a circle perpendicular to the x axis, at a position given by x above The item was titled "The Saving Ingredient", and the equation letters were not capitalized 4 Professor Albert Einstein, in the course of a newspaper interview, offered his idea of success in life in the following formula "If a is success in life, I should say that the formula is a equals x plus y plus z, x being work and y being play"3 ψ(x,y,z) =Asin n xπx L x ⎛ The θequation is known as the associated Legendre equation, and the physically acceptable 6 solutions are the associated Legendre functions of the first kind,P l m l(θ) Note that these functions depend on both l and m l
Let us consider LHS of the equation LHS = x 3 y 3 z 3 – 3xyz LHS = 1 3 2 3 3 3 – 3(1 × 2 × 3) LHS = 1 8 27 – (3 ×6) LHS = 36 – 18That is, it lies 3 units along the positive zaxis from the xyplane On the other hand,Show that f(z) is constant on the circle x2 y2 − ax = 0, a is a real constant Solution Write the equation of the circle as x − a 2 2 y2 = a 2 2 which reveals that the circle is centered at a 2,0 and has radius a 2 A possible parametric representation of the circle is x = a 2 (1 cosθ) and y = a 2 sinθ, −π < θ ≤ π 7
X 2 4 y 2 9 z 2 = 1 Multiply both sides of the equation by 36, the least common multiple of 4,9 Multiply both sides of the equation by 3 6, the least common multiple of 4, 9 36x^ {2}9y^ {2}4z^ {2}=36 3 6 x 2 9 y 2 4 z 2 = 3 6 Subtract 36x^ {2} from3 Describe geometrically the set of points (x,y,z) that satisfy y = −3 4 Describe geometrically the set of points (x,y,z) that satisfy x y = 2 5 The equation x y z = 1 describes some collection of points in R3 Describe and sketch the points that satisfy x y z = 1 and are in the xy plane, in the xz plane, and in the yz plane 6Find the x, y, and z intercepts {by substituting 0 in for the other variables} connect the three intercepts with a triangle Graph the equation x y z = 3 When a line intercepts an axis, the value of the other variables are zero xintercept x y z = 3 {the equation} x 0 0 = 3 {substituted 0 for y and z} x = 3 {combined like terms}




11 Graphing Points In 3d Intro To 3d Functions 3d Coordinates Xyz System Youtube




Solving Linear Systems With 3 Variables No Solution Video Khan Academy
Mathematics Menu The following are algebraix expansion formulae of selected polynomials Square of summation (x y) 2 = x 2 2xy y 2 Square of difference (x y) 2 = x 2To ask Unlimited Maths doubts download Doubtnut from https//googl/9WZjCW Verify that `x^3y^3z^33x y z=1/2(xyz)(xy)^2(yz)^2(zx)^2`Z = 3 10t L 2 x = s y = 6 2s;



Systems Of Equations In Three Variables




Cramer S Rule With Three Variables Chilimath
(xyz)^3 (x y z) (x y z) (x y z) We multiply using the FOIL Method x * x = x^2 x * y = xy x * z = xz y * x = xyIn three dimensions, the solution set of an equation involving x, y and/or z is a surface Example The equation z = 3 describes a plane that is parallel to the xyplane, and is 3 units \above" it; Explanation (x −y)3 = (x − y)(x −y)(x −y) Expand the first two brackets (x −y)(x − y) = x2 −xy −xy y2 ⇒ x2 y2 − 2xy Multiply the result by the last two brackets (x2 y2 −2xy)(x − y) = x3 − x2y xy2 − y3 −2x2y 2xy2 ⇒ x3 −y3 − 3x2y 3xy2




Formula According To Blender To Create An Enneper Order 3 Blender Stack Exchange




If X Y Z 0 Show That X 3 Y 3 Z 3 3xyz With Video
No integers x;y;z with xyz6= 0 satisfy x3 y3 z3 = 0 Proof We may assume that x, y, and zare pairwise coprime If xyzis not divisible by 3, then the equation has no solution even in Z=(9), where every nonzero cube is 1 Suppose then, without loss of generality, that 3jz We will work in the UFD R= Z with = ( 1i p 3)=2, a root of the(03) L 1 x = 4 2t;Steps for Solving Linear Equation x y z = x y z x y z = x y z Subtract xyz from both sides Subtract x y z from both sides xyzxyz=0 x y z − x y z = 0 Subtract y from both sides Anything subtracted from zero gives its negation




How To Graph 3d Xyz Data Inside Excel Mesh Surface And Scatter Plot




Eclectic Trends Eclectic Trends The Lab Trend Xyz Formula 2 Eclectic Trends
An ellipsoid is a surface that may be obtained from a sphere by deforming it by means of directional scalings, or more generally, of an affine transformation An ellipsoid is a quadric surface; A rugby football (or, to a lesser extent, a North American football, which is a bit too pointed) is a good approximation to a prolate spheroid The Equation to the prolate spheroid just described is (433) x 2 a 2 y 2 c 2 z 2 c 2 = 1 Either type of spheroid can be referred to as an "ellipsoid of revolution"MATH 04 Homework Solution HanBom Moon 125Determine whether the lines L 1 x= 5 12t;




X 3 Y 3 Z 3 3xyz X Y Z X 2 Y 2 Z 2 Xy Yz Zx A 3 B 3 C 3 3abc A B C A 2 B 2 C 2 Ab Ca Youtube




How To Graph Xyz Data In 3d Inside Microsoft Excel Gray Technical Llc
Z = 1 2 (04) 5s are parallel Solution Reading o the coe cients of the parameters t and s, we see that v 1 = 2i 4j 10k and v 2 = i 2j 5k are the direction vectors for L 1 and L 2 Because v 1 = 2v 2, we conclude that the lines are parallel Example 06Equation of a plane1 3t and L 2 x= 38s;Factor x^3y^3 x3 − y3 x 3 y 3 Since both terms are perfect cubes, factor using the difference of cubes formula, a3 −b3 = (a−b)(a2 abb2) a 3 b 3 = ( a




How To Create Cross Section With Coordinates Xyz Nez Calculation Wi



How Can I Generate An Object From A Mathematical Function Blender Stack Exchange
W = f(x;y;z) where x, y and z are the independent variables For example, w = xsin(y 3z) Partial derivatives are computed similarly to the two variable case For example, @w=@x means difierentiate with respect to x holding both y and z constant and so, for this example, @w=@x = sin(y 3z) Note that a function of three variables does notGeneric formula = IF(AND(OR( A1 = x, A1 = y ), B1 = z ),"yes","no") Summary To apply more complex logic like "if cell is (x OR y) AND z", you can embed the AND and OR functions directly in the logical test of the IF function In D5, the formula is = IF(AND(OR( B5 = "red", B5 = "green"), C5 > 10),"x","") This formula returns "x" if the color inAnswered 1 year ago Author has 44K answers and 14M answer views (XYZ)^3 Put XY = A (AZ)^3= A^3 Z^3 3AZ ( AZ) = (XY)^3 Z^3 3 A^2 Z 3A Z^2 = X^3Y^3 Z^3 3 X^2 Y 3 X Y^2 3 (XY)^2 Z 3 (XY) Z^2 =X^3 Y^3 Z^3 3 X^2Y 3XY^2 3 ( X^2 Y^2 2XY ) Z 3X Z^2 3YZ^2



Surface Area




X Y Z Are Three Real Numbers X Y And Z 0 If A X Y Y Z B X Z Y
X y is a binomial in which x and y are two terms In mathematics, the cube of sum of two terms is expressed as the cube of binomial x y It is read as x plus y whole cube It is mainly used in mathematics as a formula for expanding cube of sum of any two terms in their terms ( x y) 3 = x 3 y 3 3 x 2 y 3 x y 2Click here👆to get an answer to your question ️ Using the identity and proof x^3 y^3 z^3 3xyz = (x y z)(x^2 y^2 z^2 xy yz zx)3 Use the X by Y by Z formula This is the crux of the advice by Laszlo Bock, a former Google senior vice president of personnel operations




Warm Up Evaluate For X 2 Y 3 And Z 1 1 X2 2 Xyz 3 X2 Yz Ppt Download




Warm Up Evaluate For X 2 Y 3 And Z 1 1 X2 2 Xyz 3 X2 Yz Ppt Download
Z= 72s are parallel, skew, or intersecting If they intersect, find the point of intersectionYou can put this solution on YOUR website! If =, where A, B, C, x, y, and z are nonzero integers with x, y, z ≥ 3, then A, B, and C have a common prime factor Equivalently, The equation = has no solutions in nonzero integers and pairwise coprime integers A, B, C if x, y, z ≥ 3 The conjecture was formulated in 1993 by Andrew Beal, a banker and amateur mathematician, while investigating generalizations of




You The Chemistry Detective Have Obtained A Water Insoluble Ionic Compound With The Formula Xyz3 Where X Homeworklib




Lesson 9 8 Warm Up Evaluate For X 2 Y 3 And Z X 2 2 Xyz 3 X 2 Yz4 Y Xz 4 5 X 6 Z 2 Xy Ppt Download
453 Perform implicit differentiation of a function of two or more variables In singlevariable calculus, we found that one of the most useful differentiation rules is the chain rule, which allows us to find the derivative of the composition of two functions The same thing is true for multivariable calculus, but this time we have to deal(x y) 3 = x 3 3x 2 y 3xy 2 y 3 Example (1 a 2 ) 3 = 1 3 31 2 a 2 31(a 2 ) 2 (a 2 ) 3 = 1 3a 2 3a 4 a 6 (x y z) 2 = x 2 y 2 z 2 2xy 2xz 2yzMultiply each term in y z = x y z = x by z z Cancel the common factor of z z Tap for more steps Cancel the common factor Rewrite the expression Rewrite the equation as x z = y x z = y Divide each term by x x and simplify Tap for more steps Divide each term in x z = y x z = y by x x




Number In Bravais 3 Plur 4 P Q R 13 A Compound Formed By Elements X Y And




Given Triangle Xyz With Vertices X 3 3 Y 3 3 Chegg Com
Derivation of formulas for dS z=z (x,y) R S dx dS dy Refer to the pictures at the right The surface S lies over its projection R, a region in the xyplane We divide up R into infinitesimal rectangles having area dxdy and sides parallel to the xyaxes — one of these is shownY = 1 4t;\X^3\frac{119}{48}X Z^2\frac{}{864}Z^3Y^2 Z=81(x^3 y^3 z^3 3x^2(yz) 3y^2(zx) 3z^2(xy) 5xyz)\ The new equation is \(x^3\frac{119}{48}x z^2\frac{}{864}z^3y^2 z=0\)
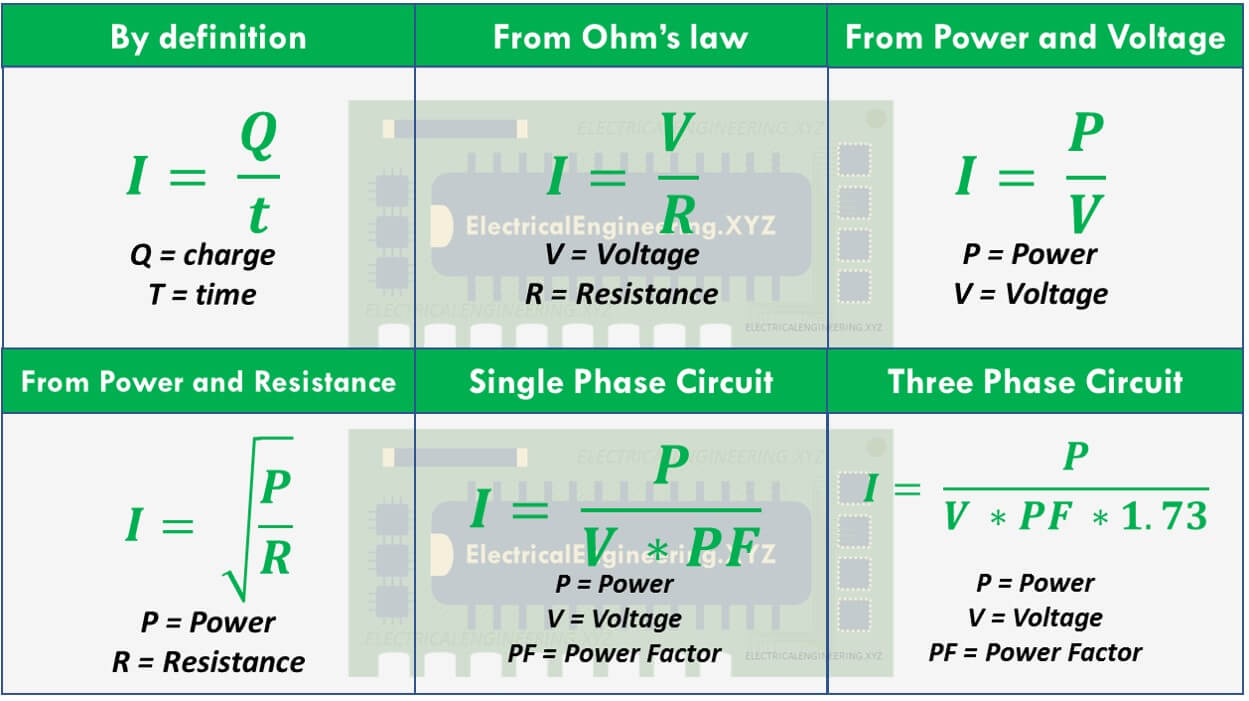



Electric Current Formula Electricalengineering Xyz Formulas
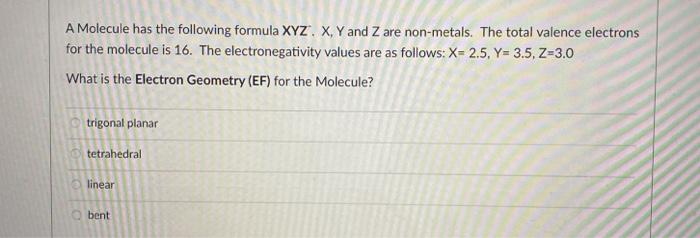



A Molecule Has The Following Formula Xyz X Y And Z Chegg Com
If the polynomial k 2 x 3 − kx 2 3kx k is exactly divisible by (x3) then the positive value of k is ____ dy dt = − sint Now, we substitute each of these into Equation 1452 dz dt = ∂z ∂x ⋅ dx dt ∂z ∂y ⋅ dy dt = (8x)(cost) (6y)( − sint) = 8xcost − 6ysint This answer has three variables in it To reduce it to one variable, use the fact that x(t) = sint and y(t) = cost We obtainX^3y^3z^33xyz=(xyz)(x^2y^2z^2xyyzzx)a^3b^3c^33abc=(abc)(a^2b^2c^2abbcca)a^3b^3c^33abc formula proofx^3y^3z^33xyz formula proofa



Formula For X Y Z 2 Brainly In



Solved Following Information For Questions 2 And Xyz Inc Uses The Average Cost Formula In A Perpetual Inventory System In Your Answer Use Unf Course Hero
The example shows 3 criteria (begins with x, y, or z) , but you add more criteria as needed Conditional formatting Since this formula returns TRUE / FALSE, you can use it asis to highlight values using conditional formatting L (x – x 1)/l = (y – y 1)/m = (z – z 1)/n Where (x, y, z) are the position coordinates of any variable point lying on the straight line Example 1 If a straight line is passing through the two fixed points in the 3dimensional whose position coordinates are P (2, 3, 5) and Q (4, 6, 12) then its cartesian equation using the twopoint form is given byThat is, a surface that may be defined as the zero set of a polynomial of degree two in three variables Among quadric surfaces, an ellipsoid is characterized by either of the two following properties Every
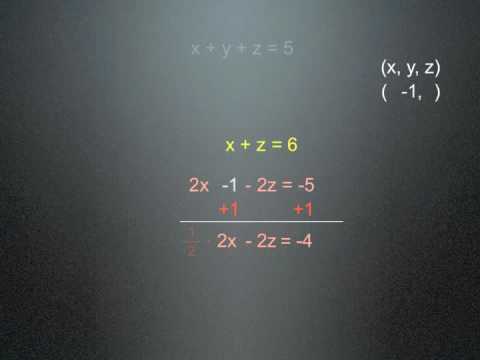



Algebra Solving Three Equations X Y And Z In Algebra Youtube




Bits Of Math Problem Cubes And Cube Roots
The triple integral of f over B is defined as ∭ B f ( x, y, z) d V = lim Δ V → 0 ∑ i = 1 m ∑ j = 1 n ∑ k = 1 l f ( x i j k ∗, y i j k ∗, z i j k ∗) ⋅ Δ V, where the triple Riemann sum is defined in the usual way The definition of the triple integral naturally extends to nonrectangular solid regions1803 Di erence Equations and ZTransforms 6 Transient If a system is stable then y hn !0 for all initial conditionsIn this case we call y h the transient Exponential Input Theorem A solution to P(R)y= an is yn = an P(a 1) Proof Ran = a n1 = a 1a )P(R)an = P(a 1)an (see below for the extended version of this theorem)Example The point x =3,y =0,andz = 1 is a solution of the following system of three linear equations in three variables 3x 2y5z = 14 2x 3y4z =10 x y z =4 That's because we can substitute 3, 0, and 1 for x, y,andz respectively in the equations above and check that 3(3) 2(0)5(1) = 95=14 2(3) 3(0)4(1) = 64 = 10 (3) (0) (1) = 31 = 4




Resume Formula Guides Examples



Equations Of Lines And Planes
Equationcalculator xyz=6, 2xyz=3, 3xz=0 en Related Symbolab blog posts High School Math Solutions – Quadratic Equations Calculator, Part 1 The formula of x 3 y 3 z 3 – 3xyz is written as \(x^{3} y^{3} z^{3} – 3xyz = (x y z) (x^{2} y^{2} z^{2} – xy – yz – zx)\) Let us prove the equation by putting the values of x = 1; What must be subtracted from 4x^42x^36x^22x6 so that the result is exactly divisible by 2x^2x1?




Covariance Formula Examples How To Calculate Correlation
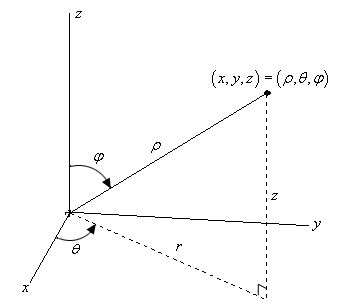



Calculus Iii Spherical Coordinates
This 3 equations 3 unknown variables solver computes the output value of the variables X and Y with respect to the input values of X, Y and Z coefficients In mathematic calculations, there are many situation arises where the usage of equation containing 3 unknown variables need to be solved prior to go further with the calculations Therefore when it comes to online calculation,Assume instead that $x, y, z\in\mathbb Z\smallsetminus\{0\}$ satisfy the equation (replacing $z$ by $z$) $$x^3 y^3 z^3 = 0,$$ with $x, y$ and $z$ pairwise coprime (Clearly at least one is negative) One of them should be even, whereas the other two are odd Assume $z$ to be even Then $x$ and $y$ are oddI'm trying to factorise $$ x^3z x^3y y^3z yz^3 xy^3 xz^3 $$ into four linear factors By plugging it into WolframAlpha I've learned that it's $$(xy)(xz)(yz)(xyz)$$ My question is




Q 1 Prove That 2x 3 2y 3 2z 3 6xyz X Y Z Formula X Y 2 Y Z 2 Z X 2 Maths Polynomials Meritnation Com



Fig S7 2d Xy Slices From Mri Xyz Of A Bulk Metal Strip Download Scientific Diagram



Plos One Excellent Accuracy Of Abc 2 Volume Formula Compared To Computer Assisted Volumetric Analysis Of Subdural Hematomas



Solution Points A 1 0 B 3 7 And C 5 2 Are The Midpoints Of The Sides Yz Zx And Xy Of Triangle Xyz Find The Equation Of The Line Xy



2




X Y 3 Y Z 3 Z X 3 3 X Y Y Z Z X 2 X3 Y3 Z3 3xyz Mathematics Topperlearning Com T86qex55




Right Triangle Xyz Has Vertices X 1 4 And Y 2 3 The Vertex Z Has Positive Integer Coordinates And X 5 Find The Coordinates Of Z And Solve Xyz Give Exact Answers Study Com




Multirow Formula For Duplicate Values Alteryx Community




Chapter 9 Xyz Custom Plus
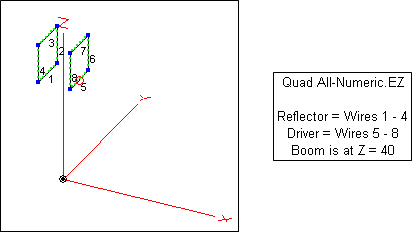



Autoez Replace Xyz Numbers In Existing Models With Formulas



Choise Of Coordinates Xyz And X Y Z Download Scientific Diagram




Find The Value Of X Y And Z Calculator




Recruiters Tips Using The X Y Z Formula On Your Resume Math Online Tom Circle



Systems Of Equations In Three Variables
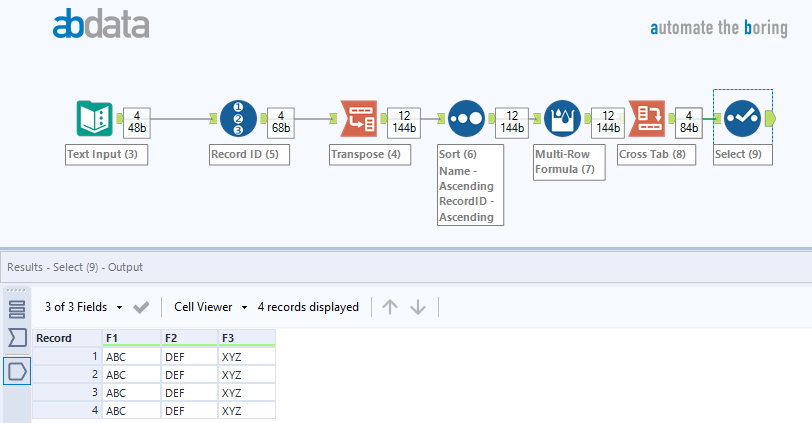



Solved Batch On Multi Row Formula Alteryx Community




A Compound Contains Atoms X Y And Z The Oxidation Number Of X Is 3 Y Is 5 And Z Is 2 The Possible Formula Of The Compound Is




If X Y Z 0 Then Show That X Cube Y Cube Z Cube 3xyz Mathematics Topperlearning Com Vj2f0044
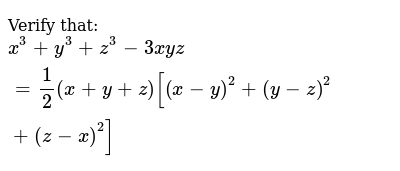



Verify That X Y Z X Z Y Z If X 4 5 Y 2 3and Z 4



1



Replace Function Xl N Cad




Lesson 9 8 Warm Up Evaluate For X 2 Y 3 And Z X 2 2 Xyz 3 X 2 Yz4 Y Xz 4 5 X 6 Z 2 Xy Ppt Download



Solution Amp 8710 Xyz Has Vertices X 0 3 Y 2 0 And Z 4 2 If You Reflect Amp 8710 Xyz Across The Line X 4 What Will Be The Coordinates Of The Vertices Of The Image




Finding X Y Z Of A Triangle Mathematics Stack Exchange




Solved A The Equation Xyz E Y Z 3 Defines Z Chegg Com




Plotting Points In Three Dimensions Krista King Math Online Math Tutor
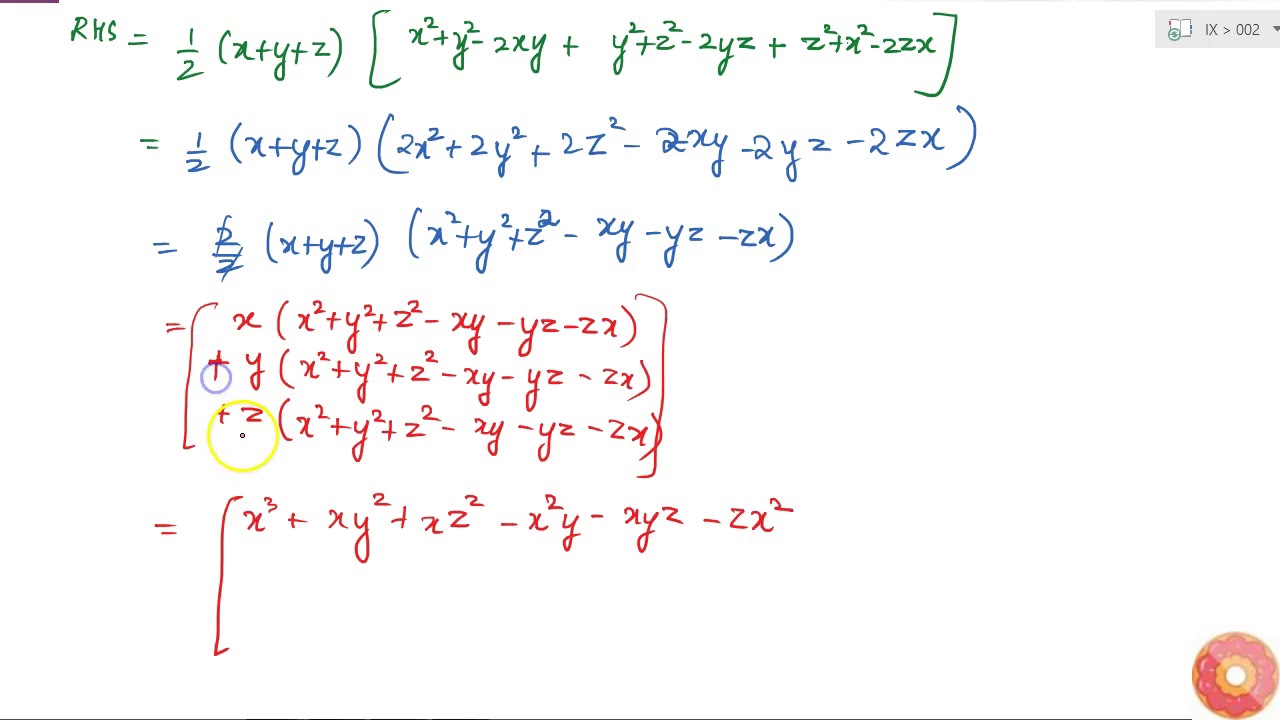



Verify That X 3 Y 3 Z 3 3x Y Z 1 2 X Y Z X Y 2 Y Z 2 Z X 2 Youtube



1




Formula According To Blender To Create An Enneper Order 3 Blender Stack Exchange




Formulas For Explaining The Natural Formula For The Application Of Xyz Download Scientific Diagram




How To Convert Distance Azimuth Dip To Xyz Newbedev




A Crystal Is Made By Using Particles X Y And Z Particle Z Forms Ccp




If Three Elements X Y And Z Crystallise Physical Chemistry
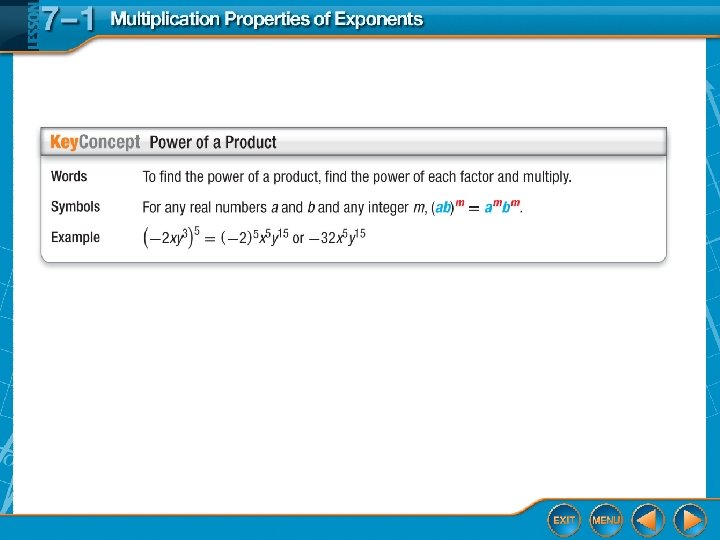



Fiveminute Check Over Chapter 6 Ccss Thennow New




The Formula For The Cross Product Math Insight




Gallery Of Xyz Formula Wgnb 3



Three Dimensional Space Wikipedia
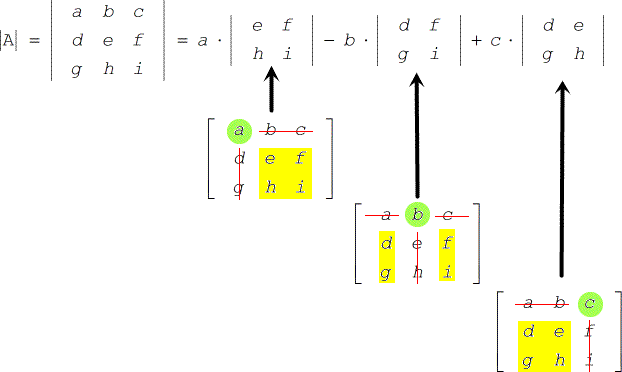



Cramer S Rule With Three Variables Chilimath




Abc And Xyz Analysis In Excel With Example Of Calculation




Solving Linear Systems With 3 Variables Video Khan Academy




The Pmj Cpu Utilisation Vs Power Consumption Destination Pmj Thus Download Scientific Diagram




Misc 16 Solve Equations 2 X 3 Y 10 Z 4 4 X 6 Y 5 Z 1




Solved Function Takes Three Parameters X Y Z Calculate Following Formula X Yl Output X Y Z Float Q Essaytaste
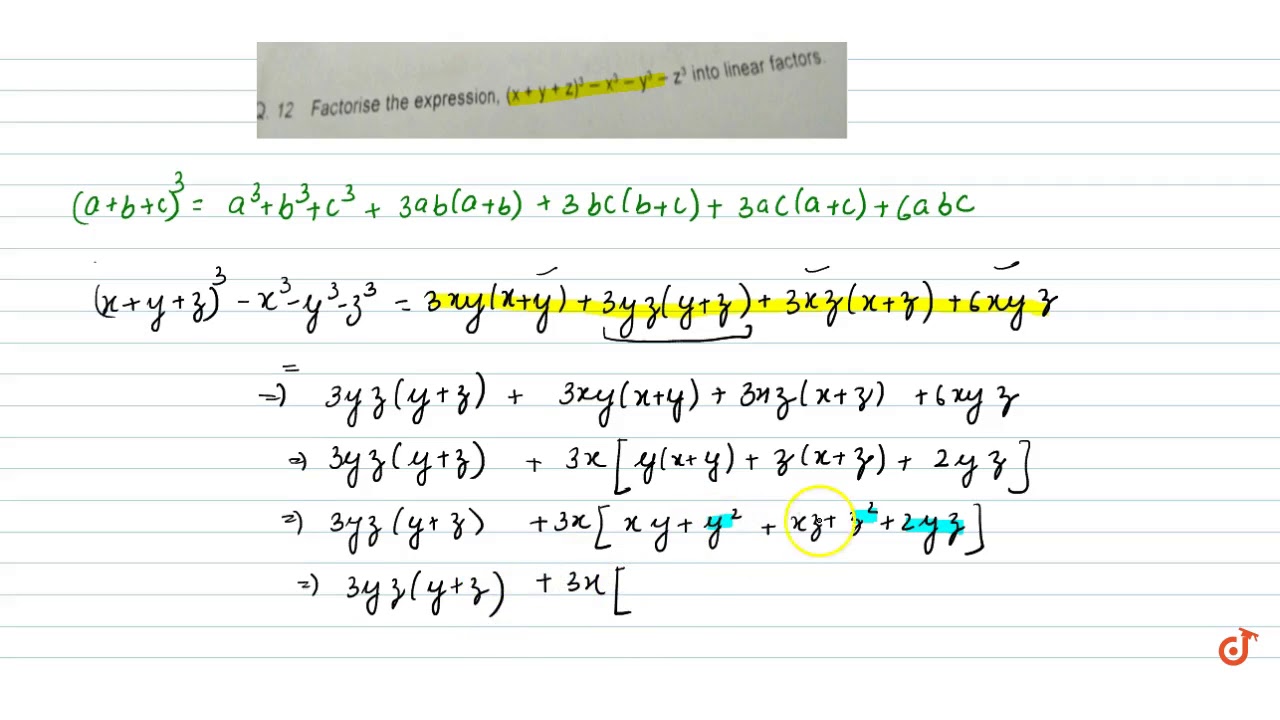



Q 12 Factorise The Expression X Y Z 3 X3 Y3 Z3 Into Linear Factors Youtube




Crystal Would Be 1 Xyz 18 2 X Yz2 4 X Y Z 1 Closest Only 3 Formula




The Distance And Midpoint Formulas Goal 1 Find




Y Verify That X 3 Y 3 Z 3 3 X Y Z Frac 1 Lambda X Y Z Left Begin Array C X Y 2 Y Z 2 Z X 2 Y Cdot 2 2 Y Z Z 2 End Array Right



Motions Of Formula 1 Car




Solved 3 Solve Defined System Equations Check Solution Su



Systems Of Equations In Three Variables




A Compound Containing X Y And Z Atoms Oxidation No Of X Is 3 Y Is 5 And Z Is 1 Then The Possible Formula Of Compound Is 1 Xyz 2 Xyz 3 X Yz 4 Xy




The Formula For Luck Leave Nothing To Chance Ten Powerful Principles For Building A Luck Mindset Lacey Stuart Ismail Salim Amazon Com Books



The Three Dimensional Coordinate System




Jacobian In Three Variables To Change Variables Krista King Math Online Math Tutor




Question 14 Xyz Company Uses The Formula Y A Bx To Predict And Analyze Homeworklib




Ii Solving A Given Two Angles Of Triangle Xyz S Gauthmath




What Is The Formula Of X Y Z 3




8 Maths Tricks Ideas Maths Solutions Math Tricks Math
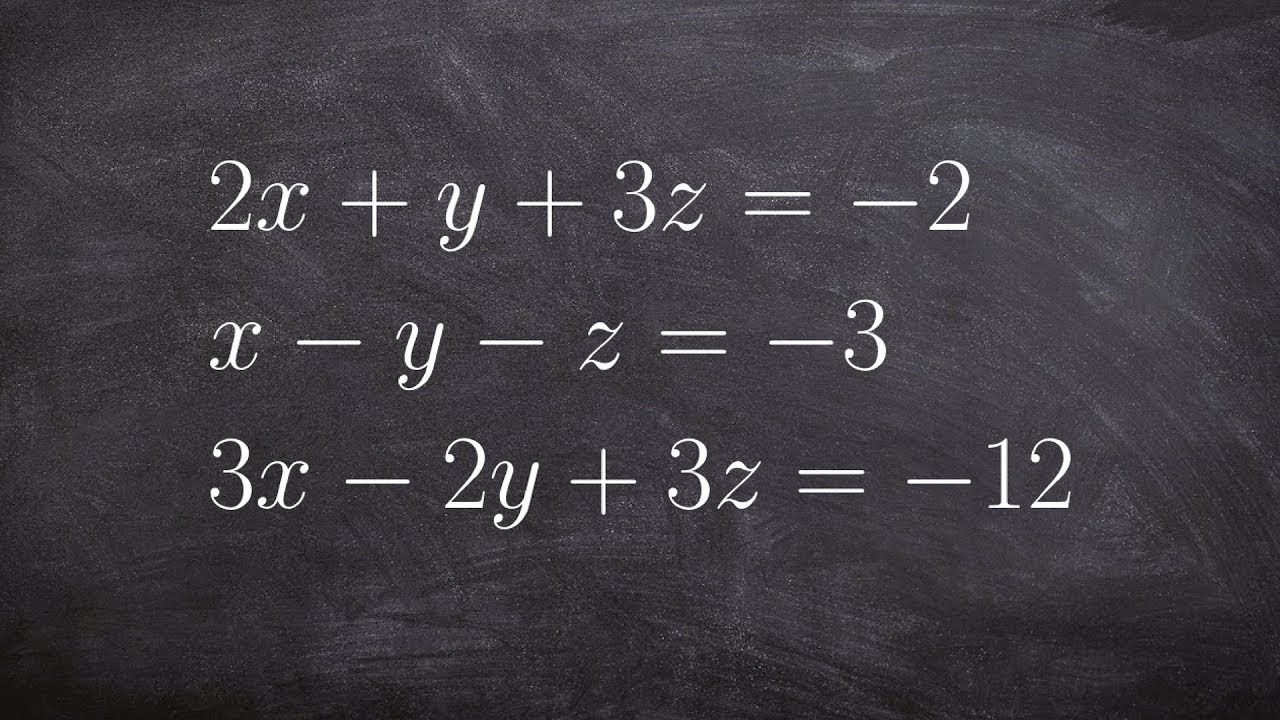



Solve A System Of Equations With Three Variables Youtube




Solving Linear Systems With 3 Variables No Solution Video Khan Academy




X Y Z Formula Math Mathematics Info



2




Lesson 9 8 Warm Up Evaluate For X 2 Y 3 And Z X 2 2 Xyz 3 X 2 Yz4 Y Xz 4 5 X 6 Z 2 Xy Ppt Download
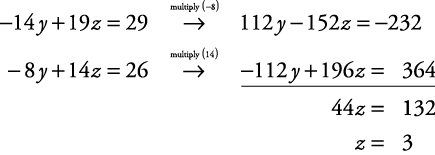



Linear Equations Solutions Using Elimination With Three Variables
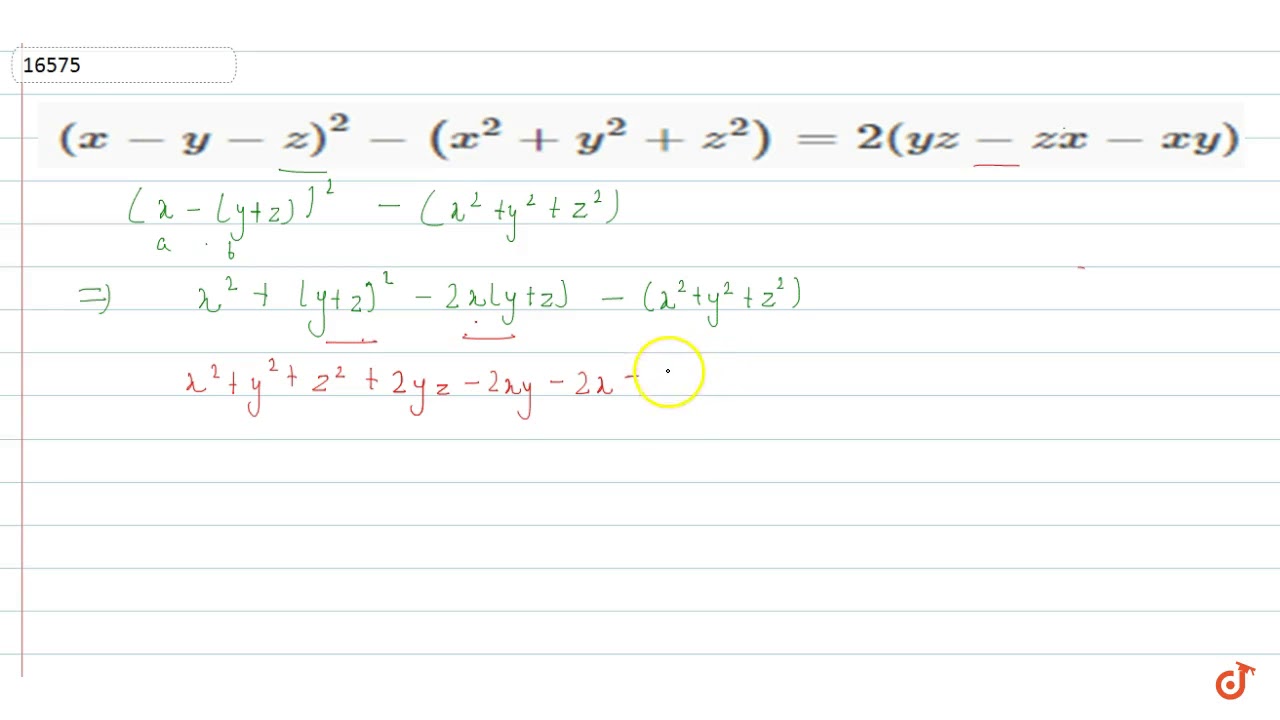



X Y Z 2 X 2 Y 2 Z 2 2 Yz Zx Xy Youtube




You The Chemistry Detective Have Obtained A Water Insoluble Ionic Compound With The Formula Xyz3 Where X Homeworklib




If X Y Z 0 Show That X3 Y3 Z3 3 Xyz Brainly In




Solving Systems Of Linear Equations In Three Variables Using Determinants Video Lesson Transcript Study Com



Solved Xyz Limited Is A Manufacturer Of Chocolate In Europe The Company Aims To Provide High Quality Product And Unique Experience For Consumers Course Hero




Graphing A Plane On The Xyz Coordinate System Using Traces Youtube



Systems Of Equations In Three Variables




Holt Algebra The Quadratic Formula And The Discriminant Warm Up Add To Hw Pass Back Papers Evaluate For X 2 Y 3 And Z X Ppt Download
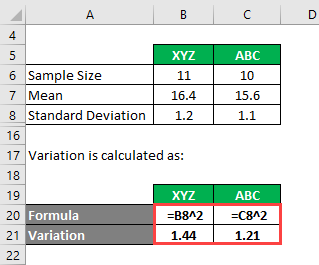



F Test Formula How To Calculate F Test Examples With Excel Template



No comments:
Post a Comment